Question

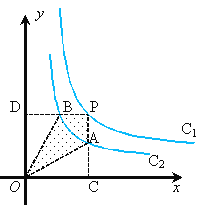
【题目】如图，两个反比例函数C1:y=和C2:y=在第一象限内的图象如图，P在C1上作PC、PD垂直于坐标轴，垂线与C2交点为A、B，则下列结论，其中正确的是( )

①△ODB与△OCA的面积相等；②四边形PAOB的面积等于k1- k2；③PA与PB始终相等；④当点A是PC的中点时，点B一定是PD的中点

A. ①② B. ②④ C. ①②④ D. ①③④

【答案】C

【解析】①∵A、B两点都在y=上，∴△ODB与△OCA的面积都都等于，则①正确；②S矩形OCPB-S△AOC-S△DBO=|k2|-2×|k1|÷2=k2-k1，则②正确；③只有当P的横纵坐标相等时，PA=PB，错误；④当点A是PC的中点时，点B一定是PD的中点，正确．故选C．

【题型】单选题
【结束】
10

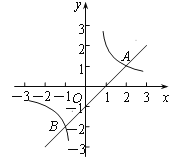
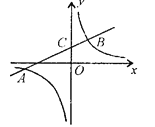
【题目】如图，反比例函数（k＞0）与一次函数的图象相交于两点A(,),B(,),线段AB交y轴与C，当|－ |=2且AC = 2BC时，k、b的值分别为（ ）

A. k＝,b＝2 B. k＝,b＝1 C. k＝,b＝ D. k＝,b＝

Answer 1

【答案】D

【解析】∵AC=2BC，∴A点的横坐标的绝对值是B点横坐标绝对值的两倍．∵点A、点B都在一次函数y＝x+b的图象上，∴设B（m， m+b），则A（-2m，-m+b），∵|－|=2，∴m-(-2m)=2，解得m=，又∵点A、点B都在反比例函数的图象上，∴（+b）=(-)×（-+b），解得b=，∴k=×（+）=，故选D.