题目内容
【题目】如图,已知点A. B在双曲线y=![]() (x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.
(x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.
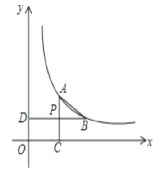
(1)设A的横坐标为m,试用m、k表示B的坐标.
(2)试判断四边形ABCD的形状,并说明理由.
(3)若△ABP的面积为3,求该双曲线的解析式.
【答案】(1)B(2m,![]() );(2)四边形ABCD是菱形,理由见解析;(3)y=
);(2)四边形ABCD是菱形,理由见解析;(3)y=![]() .
.
【解析】
(1)根据点P是AC的中点得到点A的横坐标是m,结合反比例函数图象上点的坐标特征来求点B的坐标;
(2)根据点P的坐标得到点P是BD的中点,所以由“对角线互相垂直平分的四边形是菱形”得到四边形ABCD是菱形;
(3)由△ABP的面积为3,知BPAP=6.根据反比例函数 y=![]() 中k的几何意义,知本题k=OCAC,由反比例函数的性质,结合已知条件P是AC的中点,得出OC=BP,AC=2AP,进而求出k的值.
中k的几何意义,知本题k=OCAC,由反比例函数的性质,结合已知条件P是AC的中点,得出OC=BP,AC=2AP,进而求出k的值.
(1)∵A的横坐标为m,AC⊥x轴于C,P是AC的中点,
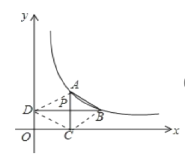
∴点B的横坐标是2m.
又∵点B在双曲线y=![]() (x>0)上,
(x>0)上,
∴B(2m,![]() ).
).
(2)连接AD、CD、BC;
∵AC⊥x轴于C,BD⊥y轴于点D,
∴AC⊥BD;
∵A(m,![]() ),B(2m,
),B(2m, ![]() ),
),
∴P(m, ![]() ),
),
∴PD=PB,
又AP=PC,
∴四边形ABCD是菱形;
(3)∵△ABP的面积为![]() BPAP=3,
BPAP=3,
∴BPAP=6,
∵P是AC的中点,
∴A点的纵坐标是B点纵坐标的2倍,
又∵点A. B都在双曲线y=![]() (x>0)上,
(x>0)上,
∴B点的横坐标是A点横坐标的2倍,
∴OC=DP=BP,
∴k=OCAC=BP2AP=12.
∴该双曲线的解析式是:y=![]() .
.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】八年 2 班组织了一次经典诵读比赛,甲乙两组各 10 人的比赛成绩如下表(10 分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(Ⅰ)甲组数据的中位数是 ,乙组数据的众数是 ;
(Ⅱ)计算乙组数据的平均数和方差;
(Ⅲ)已知甲组数据的方差是 1.4 分,则成绩较为整齐的是 。