题目内容
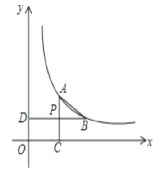
【题目】如图，在平面直角坐标系中，四边形ABCD的顶点都在格点上，其中A点坐标为（﹣2，﹣1），C点坐标为（3，3）．
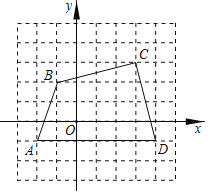
（1）填空：点B到y轴的距离为 ，点B到直线AD的距离为 ；
（2）求四边形ABCD的面积；
（3）点M在y轴上，当△ADM的面积为12时，请直接写出点M的坐标．
【答案】（1）1，3；（2）
；（3）M（0，﹣5），（0，3）.
【解析】
（1）根据图形即可得到结论；
（2）根据矩形和三角形的面积公式即可得到结论；
（3）根据三角形的面积列方程即可得到结论．
解：（1）根据图形可知，B（﹣1，2），
∴点B到y轴的距离为1，点B到直线AD的距离为3；
故答案为：1，3；
（2）四边形ABCD的面积＝6×4﹣
×3×1﹣×4×1﹣×1×4-1＝；
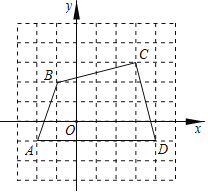
（3）设点M的坐标（0，m），
∵△ADM的面积为12，
∴×6×|m+1|＝12，
∴m＝3或-5，
∴M（0，﹣5），（0，3）．
练习册系列答案
相关题目
【题目】（2013年四川广安8分）某商场筹集资金12.8万元，一次性购进空调、彩电共30台．根据市场需要，这些空调、彩电可以全部销售，全部销售后利润不少于1.5万元，其中空调、彩电的进价和售价见表格．
空调 | 彩电 | |
进价（元/台） | 5400 | 3500 |
售价（元/台） | 6100 | 3900 |
设商场计划购进空调x台，空调和彩电全部销售后商场获得的利润为y元．
（1）试写出y与x的函数关系式；
（2）商场有哪几种进货方案可供选择？
（3）选择哪种进货方案，商场获利最大？最大利润是多少元？
