题目内容
如图,AB是⊙O的直径,直线AD与⊙O相切于点A,点C在⊙O上,∠DAC=∠ACD,直线DC与AB的延长线交于点E.AF⊥ED于点F,交⊙O于点G.
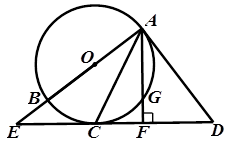
⑴ 求证:DE是⊙O的切线;
⑵ 已知⊙O的半径是6cm,EC=8cm, 求GF的长.
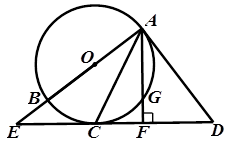
⑴ 求证:DE是⊙O的切线;
⑵ 已知⊙O的半径是6cm,EC=8cm, 求GF的长.
(1)证明:联结OC.
∵AD是⊙O的切线,∴∠OAD=90°,
∴∠OAC+∠DAC=90°.
∵OA=OC,∴∠OAC=∠OCA.
∵∠DAC=∠ACD,
∴∠OCA+∠ACD=90°,即∠OCD=90°,
∴AD是⊙O的切线.
(2)GF=2.4cm
∵AD是⊙O的切线,∴∠OAD=90°,
∴∠OAC+∠DAC=90°.
∵OA=OC,∴∠OAC=∠OCA.
∵∠DAC=∠ACD,
∴∠OCA+∠ACD=90°,即∠OCD=90°,
∴AD是⊙O的切线.
(2)GF=2.4cm
试题分析:⑴ 证明:联结OC.
∵AD是⊙O的切线,∴∠OAD=90°,
∴∠OAC+∠DAC=90°.
∵OA=OC,∴∠OAC=∠OCA.
∵∠DAC=∠ACD,
∴∠OCA+∠ACD=90°,即∠OCD=90°,
∴AD是⊙O的切线.
⑵ 联结BG,
∵OC=6cm,EC=8cm,
∴在Rt△CEO中,OE=
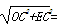 10 cm.
10 cm.∴AE="OE+OA=16" cm.
∵AF⊥ED,
∴∠AFE=∠OCE=90°,∠E=∠E.
∴Rt△AEF∽Rt△OEC.
∴
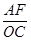 =
=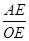 ,
,∴AF=
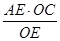 =
= ="9.6" cm.
="9.6" cm. ∵AB是⊙O的直径,∴∠AGB=90°,
∴BG∥EF,
∴
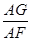 =
=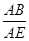 ,
,∴AG=
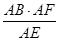 =
=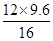 ="7.2" cm,
="7.2" cm, ∴GF=AF-AG=9.6-7.2=2.4cm.
点评:本题考查了切线的性质和判定,相似三角形的性质和判定,主要考查学生能否运用性质进行推理和计算,难度中等。

练习册系列答案
相关题目

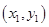 、P2
、P2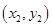 在反比例函数
在反比例函数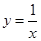 (x>0)的图象上,则
(x>0)的图象上,则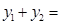 __________.
__________.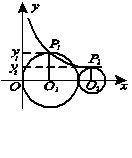
 ,母线长为
,母线长为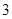 ,则这个圆锥的侧面积是 .(结果保留
,则这个圆锥的侧面积是 .(结果保留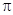 )
)
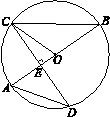
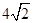 ,AE=2,求⊙O的半径.
,AE=2,求⊙O的半径.