题目内容
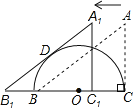
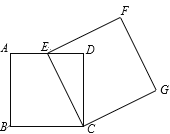
【题目】如图,正方形ABCD与正方形CEFG,E是AD的中点,若AB=2,则点B与点F之间的距离为_______.
【答案】3![]()
【解析】
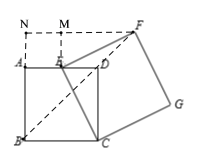
过点F作FN⊥BA,交BA延长线于N,过点E作EM⊥FN于M,连接BF,可得四边形AEMN是矩形,由直角三角形两锐角互余的关系可得∠FEM=∠CED,利用AAS可证明△FEM≌△CED,可得DE=EM,FM=CD,即可求出MN和AN的长,进而可求出FN和BN的长,利用勾股定理求出BF的长即可.
过点F作FN⊥BA,交BA延长线于N,过点E作EM⊥FN于M,连接BF,
∵点E为AD中点,AD=AB=CD=2,
∴AE=ED=1,
∵FN⊥BN,DA⊥BN,EM⊥FN,
∴四边形AEMN是矩形,
∴MN=AE=1,
∴∠FEM+∠FED=90°,
∵∠FED+∠CED=90°,
∴∠FEM=∠CED,
又∵∠EMF=∠EDC=90°,EF=CE,
∴△FEM≌△CED,
∴EM=ED=1,FM=CD=2,
∴AN=EM=1,
∴FN=FM+MN=3,BN=AB+AN=3,
∴BF=![]() =
=![]() =
=![]() .
.
故答案为:![]()

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案【题目】主题班会课上,王老师出示了如图一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟,根据同学们的选择情况,小明绘制了如图两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
观点 | 频数 | 频率 |
A | a | 0.2 |
B | 12 | 0.24 |
C | 8 | b |
D | 20 | 0.4 |

(1)参加本次讨论的学生共有 人;
(2)表中a= ,b= ;
(3)将条形统计图补充完整;
(4)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.