Question

【题目】如图，一次函数y=ax﹣1的图象与反比例函数y=的图象交于A，B两点，与x轴交于点C，与y轴交于点D，已知OA=，tan∠AOC=．

（1）求a，k的值及点B的坐标；

（2）观察图象，请直接写出不等式ax﹣1≥的解集；

（3）在y轴上存在一点P，使得△PDC与△ODC相似，请你求出P点的坐标．

Answer 1

【答案】（1）a= ,k=3, B(-,-2) (2) ﹣≤x＜0或x≥3；(3) （0，）或（0，0）

【解析】

1)过A作AE⊥x轴,交x轴于点E,在Rt△AOE中,根据tan∠AOC的值,设AE=x,得到OE=3x,再由OA的长,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出A坐标,将A坐标代入一次函数解析式求出a的值,代入反比例解析式求出k的值,联立一次函数与反比例函数解析式求出B的坐标;

(2)由A与B交点横坐标,根据函数图象确定出所求不等式的解集即可;

(3)显然P与O重合时,满足△PDC与△ODC相似;当PC⊥CD,即∠PCD=时,满足三角形PDC与三角形CDO相等,利用同角的余角相等得到一对角相等,再由一对直角相等得到三角形PCO与三角形CDO相似,由相 似得比例,根据OD,OC的长求出OP的长,即可确定出P的坐标.

解：（1）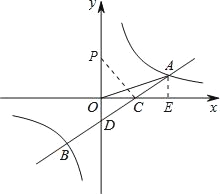

过A作AE⊥x轴，交x轴于点E，

在Rt△AOE中，OA=，tan∠AOC=，

设AE=x，则OE=3x，

根据勾股定理得：OA2=OE2+AE2，即10=9x2+x2，

解得：x=1或x=﹣1（舍去），

∴OE=3，AE=1，即A（3，1），

将A坐标代入一次函数y=ax﹣1中，得：1=3a﹣1，即a=，

将A坐标代入反比例解析式得：1=，即k=3，

联立一次函数与反比例解析式得：，

消去y得： x﹣1=，

解得：x=﹣或x=3，

将x=﹣代入得：y=﹣1﹣1=﹣2，即B（﹣，﹣2）；

（2）由A（3，1），B（﹣，﹣2），

根据图象得：不等式x﹣1≥的解集为﹣≤x＜0或x≥3；

（3）显然P与O重合时，△PDC∽△ODC；

当PC⊥CD，即∠PCD=90°时，∠PCO+∠DCO=90°，

∵∠PCD=∠COD=90°，∠PCD=∠CDO，

∴△PDC∽△CDO，

∵∠PCO+∠CPO=90°，

∴∠DCO=∠CPO，

∵∠POC=∠COD=90°，

∴△PCO∽△CDO，

∴=，

对于一次函数解析式y=x﹣1，令x=0，得到y=﹣1；令y=0，得到x=，

∴C（，0），D（0，﹣1），即OC=，OD=1，

∴=，即OP=，

此时P坐标为（0，），

综上，满足题意P的坐标为（0，）或（0，0）．