题目内容
【题目】如图,抛物线y=ax2+bx向上平移2个单位之后,正好与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
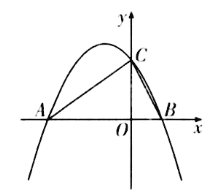
(1)求平移后抛物线的表达式;
(2)点Q是直线AC上方的抛物线上一点,过点Q作QE垂直于x轴,若以点B、Q、E为顶点的角形与△AOC相似,请求出Q点的坐标.
【答案】(1)![]() ;(2)Q(-2,2)或
;(2)Q(-2,2)或![]()
【解析】
(1)利用待定系数法求函数解析式;(2)如图所示,若以点B、Q、E为顶点的三角形与△AOC相似,有两种情况,需要分类讨论,不要漏解;
解:(1)∵抛物线y=ax2+bx向上平移2个单位
∴抛物线y=ax2+bx+2
又∵抛物线过点A(-3,0),B(1,0),
∴![]() ,
,
解得: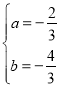 ,
,
∴二次函数的关系解析式为![]()
(2)如图所示,过点Q作QE垂直于x轴,设E(n,0),则BE=1-n,QE=![]()
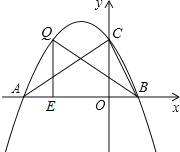
假设以点B、Q、E为顶点的三角形与△AOC相似,则有两种情况:
若△AOC∽△BEQ,则有:![]() ,
,
即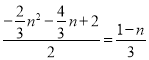 ,化简得:n2+n-2=0,
,化简得:n2+n-2=0,
解得n1=-2,n2=1(与B重合,舍去),
∴n=-2,QE=![]() =2
=2
∴Q(-2,2);
若△AOC∽△BQE,则有: ![]()
即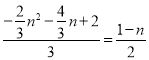 ,化简得:4n2-n-3=0,
,化简得:4n2-n-3=0,
解得n1=![]() ,n2=1(与B重合,舍去),
,n2=1(与B重合,舍去),
∴n=![]() ,QE=
,QE=![]() .
.
∴Q![]() .
.
综上所述,存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似.
Q点坐标为(-2,2)或![]()

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目