جâؤ؟ؤعبف
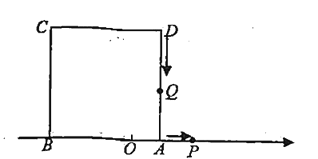
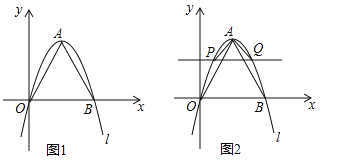
،¾جâؤ؟،؟£¨2016¼ھءضت،£©بçح¼1£¬شعئ½أوض±½ا×ّ±êدµضذ£¬µمBشعxضلص°ëضلةد£¬OBµؤ³¤¶بخھ2m£¬زشOBخھ±كدٍةد×÷µب±كب½اذخAOB£¬إ×خïدكl£؛![]() ¾¹µمO£¬A£¬Bبµم£®
¾¹µمO£¬A£¬Bبµم£®
£¨1£©µ±m=2ت±£¬a= £¬µ±m=3ت±£¬a= £»
£¨2£©¸ù¾ف£¨1£©ضذµؤ½ل¹û£¬²آدëaسëmµؤ¹طدµ£¬²¢ض¤أ÷ؤمµؤ½لآغ£»
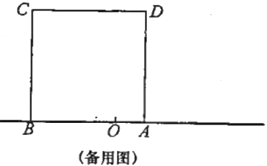
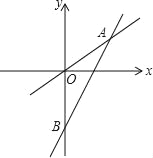
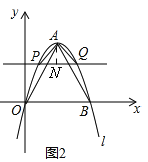
£¨3£©بçح¼2£¬شعح¼1µؤ»ù´،ةد£¬×÷xضلµؤئ½ذذدك½»إ×خïدكlسعP،¢Qء½µم£¬PQµؤ³¤¶بخھ2n£¬µ±،÷APQخھµبرüض±½اب½اذخت±£¬a؛حnµؤ¹طدµت½خھ £»
£¨4£©ہûسأ£¨2£©£¨3£©ضذµؤ½لآغ£¬اَ،÷AOBسë،÷APQµؤأو»±ب£®
،¾´ً°¸،؟£¨1£©![]() £¬
£¬![]() £»£¨2£©
£»£¨2£©![]() £»£¨3£©
£»£¨3£©![]() £»£¨4£©
£»£¨4£©![]() £؛1£®
£؛1£®
،¾½âخِ،؟تشجâ·ضخِ£؛£¨1£©سة،÷AOBخھµب±كب½اذخ£¬AB=2m£¬µأ³ِµمA£¬B×ّ±ê£¬شظسةµمA£¬B£¬Oشعإ×خïدكةد½¨ء¢·½³ج×飬µأ³ِ½لآغ£¬×î؛َ´ْm=2£¬m=3£¬اَضµ¼´؟ة£»
£¨2£©ح¬£¨1£©µؤ·½·¨µأ³ِ½لآغ
£¨3£©سة،÷APQخھµبرüض±½اب½اذخ£¬PQµؤ³¤¶بخھ2n£¬ةèA£¨e£¬d+n£©£¬،àP£¨e©پn£¬d£©£¬Q£¨e+n£¬d£©£¬½¨ء¢·½³ج×éاَ½â¼´؟ة£»
£¨4£©سة£¨2£©£¨3£©µؤ½لآغµأµ½m=![]() n£¬شظ¸ù¾فأو»¹«ت½ءذ³ِت½×س£¬´ْب뻯¼ٍ¼´؟ة£®
n£¬شظ¸ù¾فأو»¹«ت½ءذ³ِت½×س£¬´ْب뻯¼ٍ¼´؟ة£®
تشجâ½âخِ£؛½â£؛£¨1£©بçح¼1£¬،كµمBشعxضلص°ëضلةد£¬OBµؤ³¤¶بخھ2m£¬،àB£¨2m£¬0£©£®،كزشOBخھ±كدٍةد×÷µب±كب½اذخAOB£¬،àAM=![]() m£¬OM=m£¬،àA£¨m£¬
m£¬OM=m£¬،àA£¨m£¬![]() m£©£®،كإ×خïدكl£؛
m£©£®،كإ×خïدكl£؛![]() ¾¹µمO£¬A£¬Bبµم£¬،à
¾¹µمO£¬A£¬Bبµم£¬،à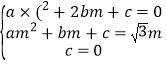 £¬،à
£¬،à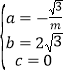 £®
£®
µ±m=2ت±£¬a=![]() £¬µ±m=3ت±£¬a=
£¬µ±m=3ت±£¬a=![]() £®¹ت´ً°¸خھ£؛
£®¹ت´ً°¸خھ£؛![]() £¬
£¬![]() £»
£»
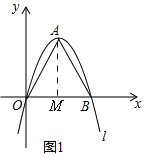
£¨2£©![]() £®ہيسة£؛بçح¼1£¬،كµمBشعxضلص°ëضلةد£¬OBµؤ³¤¶بخھ2m£¬،àB£¨2m£¬0£©£®،كزشOBخھ±كدٍةد×÷µب±كب½اذخAOB£¬،àAM=
£®ہيسة£؛بçح¼1£¬،كµمBشعxضلص°ëضلةد£¬OBµؤ³¤¶بخھ2m£¬،àB£¨2m£¬0£©£®،كزشOBخھ±كدٍةد×÷µب±كب½اذخAOB£¬،àAM=![]() m£¬OM=m£¬،àA£¨m£¬
m£¬OM=m£¬،àA£¨m£¬![]() m£©£®،كإ×خïدكl£؛
m£©£®،كإ×خïدكl£؛![]() ¾¹µمO£¬A£¬Bبµم£¬،à
¾¹µمO£¬A£¬Bبµم£¬،à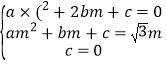 £¬،à
£¬،à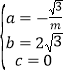 £¬،à
£¬،à![]() £»
£»
£¨3£©بçح¼2£¬،ك،÷APQخھµبرüض±½اب½اذخ£¬PQµؤ³¤¶بخھ2n£¬ةèA£¨e£¬d+n£©£¬،àP£¨e©پn£¬d£©£¬Q£¨e+n£¬d£©£®،كP£¬Q£¬A£¬Oشعإ×خïدكl£؛![]() ةد£¬،à
ةد£¬،à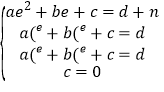 £¬،à
£¬،à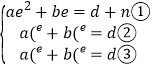 £¬¢ظ©پ¢ع»¯¼ٍµأ£¬2ae©پan+b=1¢ـ£¬¢ظ©پ¢غ»¯¼ٍµأ£؛©پ2ae©پan©پb=1¢ف£¬¢ـ+¢ف»¯¼ٍµأ£؛an=©پ1£¬،à
£¬¢ظ©پ¢ع»¯¼ٍµأ£¬2ae©پan+b=1¢ـ£¬¢ظ©پ¢غ»¯¼ٍµأ£؛©پ2ae©پan©پb=1¢ف£¬¢ـ+¢ف»¯¼ٍµأ£؛an=©پ1£¬،à![]() £®¹ت´ً°¸خھ£؛
£®¹ت´ً°¸خھ£؛![]() £®
£®
£¨4£©،كOBµؤ³¤¶بخھ2m£¬AM=![]() m£¬،àS،÷AOB=
m£¬،àS،÷AOB=![]() OB،ءAM=
OB،ءAM=![]() ،ء2m،ء
،ء2m،ء![]() m=
m=![]() £¬سة£¨3£©سذ£¬AN=n£®
£¬سة£¨3£©سذ£¬AN=n£®
،كPQµؤ³¤¶بخھ2n£¬،àS،÷APQ=![]() PQ،ءAN=
PQ،ءAN=![]() ،ء2n،ءn=
،ء2n،ءn=![]() £¬سة£¨2£©£¨3£©سذ£¬
£¬سة£¨2£©£¨3£©سذ£¬![]() £¬
£¬![]() £¬،à
£¬،à![]() £¬،àm=
£¬،àm=![]() n£¬،à
n£¬،à![]() =
=![]() =
=![]() =
=![]() £¬،à،÷AOBسë،÷APQµؤأو»±بخھ
£¬،à،÷AOBسë،÷APQµؤأو»±بخھ![]() £؛1£®
£؛1£®

 ³ُضذتîئعدخ½سدµءذ´ً°¸
³ُضذتîئعدخ½سدµءذ´ً°¸،¾جâؤ؟،؟ؤ³¾çش؛µؤ¹غضعد¯µؤ×ùخ»خھةبذخ£¬از°´دآءذ·ضت½ةèضأ£؛
إإت£¨x£© | 1 | 2 | 3 | 4 | ، |
×ùخ»ت£¨y£© | 50 | 53 | 56 | 59 | ، |
£¨1£©°´صصةد±يثùت¾µؤ¹وآة£¬µ±xأ؟شِ¼س1ت±£¬yبç؛خ±ن»¯£؟
£¨2£©ذ´³ِ×ùخ»تyسëإإتxض®¼نµؤ¹طدµت½£»
£¨3£©°´صصةد±يثùت¾µؤ¹وآة£¬ؤ³ز»إإ؟ةؤـسذ90¸ِ×ùخ»آً£؟ثµثµؤمµؤہيسة£®