题目内容
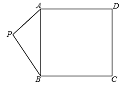
【题目】如图,已知P是正方形ABCD外一点,且PA=3,PB=4 ,则PC的最大值是________;
【答案】![]()
【解析】分析:过点B作BE⊥BP使点E在正方形ABCD的外部,且BE=PB,连接AE、PE、PC,然后求出PE=![]() PB,再求出∠ABE=∠CBP,然后利用“边角边”证明△ABE和△CBP全等,根据全等三角形对应边相等可得AE=PC,再根据两点之间线段最短可知点A、P、E三点共线时AE最大,也就是PC最大.
PB,再求出∠ABE=∠CBP,然后利用“边角边”证明△ABE和△CBP全等,根据全等三角形对应边相等可得AE=PC,再根据两点之间线段最短可知点A、P、E三点共线时AE最大,也就是PC最大.
详解:如图,过点B作BE⊥BP,且BE=PB,连接AE、PE、PC,
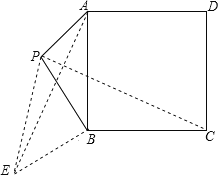
则PE=![]() PB=4
PB=4![]() ,
,
∵∠ABE=∠ABP+90,∠CBP=∠ABP+90,
∴∠ABE=∠CBP,
在△ABE和△CBP中,
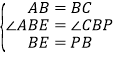 ,
,
∴△ABE≌△CBP(SAS),
∴AE=PC,
由两点之间线段最短可知,点A. P、E三点共线时AE最大,
此时AE=AP+PE=3+4![]() ,
,
所以,PC的最大值是3+4![]() .
.
故答案为:3+4![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目