题目内容
【题目】如图,矩形ABCD中,点E,F分别在边AB,CD上,点G,H在对角线AC上,EF与AC相交于点O,AG=CH,BE=DF.
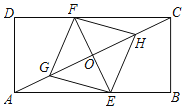
(1)求证:四边形EGFH是平行四边形;
(2)当EG=EH时,连接AF
①求证:AF=FC;
②若DC=8,AD=4,求AE的长.
【答案】(1)见解析;(2)①见解析,②5.
【解析】
(1)依据矩形的性质,即可得出△AEG≌△CFH,进而得到GE=FH,∠CHF=∠AGE,由∠FHG=∠EGH,可得FH∥GE,即可得到四边形EGFH是平行四边形;
(2)①由菱形的性质,即可得到EF垂直平分AC,进而得出AF=CF;
②设AE=x,则FC=AF=x,DF=8-x,依据Rt△ADF中,AD2+DF2=AF2,即可得到方程,即可得到AE的长.
(1)∵矩形ABCD中,AB∥CD,
∴∠FCH=∠EAG,
又∵CD=AB,BE=DF,
∴CF=AE,
又∵CH=AG,∠FCH=∠EAG
∴△AEG≌△CFH(SAS),
∴GE=FH,∠CHF=∠AGE,
∴∠FHG=∠EGH,
∴FH∥GE,
∴四边形EGFH是平行四边形;
(2)①如图,连接AF,
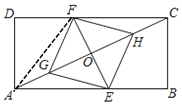
∵EG=EH,四边形EGFH是平行四边形,
∴四边形GFHE为菱形,
∴EF垂直平分GH,
又∵AG=CH,
∴EF垂直平分AC,
∴AF=CF;
②设AE=x,则FC=AF=x,DF=8-x,
在Rt△ADF中,AD2+DF2=AF2,
∴42+(8-x)2=x2,
解得x=5,
∴AE=5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目