题目内容
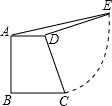 如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=5,将腰DC绕点D逆时针方向旋转90°至DE,连接AE,则△ADE的面积是( )
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=5,将腰DC绕点D逆时针方向旋转90°至DE,连接AE,则△ADE的面积是( )| A、1 | B、2 | C、3 | D、4 |
分析:求△ADE的面积,已知底AD=3,过E作EF垂直于AD交AD的延长线于F,EF就是高,然后再找和高相等的等量关系,三角形EDF全等于三角形CDG,EF=CG=2,则△ADE的面积就能求出来.
解答: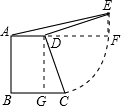 解:过点D作DG垂直于BC于G,过E作EF垂直于AD交AD的延长线于F,
解:过点D作DG垂直于BC于G,过E作EF垂直于AD交AD的延长线于F,
∵∠EDF+∠CDF=90°,∠CDF+∠CDG=90°,
∴∠EDF=∠CDG,
又∵∠EFD=∠CGD=90°,DE=DC,
∴△EDF≌△CDG(AAS),
∴EF=CG,
∴CG=BC-BG=5-3=2,
∴EF=2,
∴S△ADE=
×AD×EF=
×3×2=3.
故选C.
 解:过点D作DG垂直于BC于G,过E作EF垂直于AD交AD的延长线于F,
解:过点D作DG垂直于BC于G,过E作EF垂直于AD交AD的延长线于F,∵∠EDF+∠CDF=90°,∠CDF+∠CDG=90°,
∴∠EDF=∠CDG,
又∵∠EFD=∠CGD=90°,DE=DC,
∴△EDF≌△CDG(AAS),
∴EF=CG,
∴CG=BC-BG=5-3=2,
∴EF=2,
∴S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题需要把旋转的性质、三角形的面积公式结合求解.考查学生综合运用数学知识的能力.注意旋转变化前后,对应角相等.

练习册系列答案
相关题目
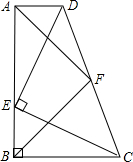 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.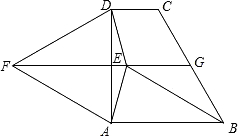 ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.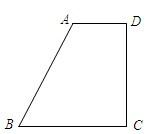 如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.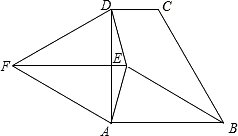 (2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.
已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.