题目内容
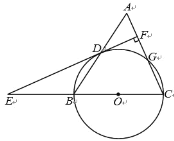
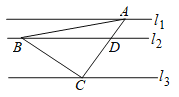
【题目】如图,直线![]() ,等腰直角三角形
,等腰直角三角形![]() 的三个顶点
的三个顶点![]() 分别在
分别在![]() ,
,![]() ,
,![]() 上,
上,![]() 90°,
90°,![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() 与
与![]() 的距离为2,
的距离为2,![]() 与
与![]() 的距离为3,则
的距离为3,则![]() 的长为________.
的长为________.
【答案】![]()
【解析】
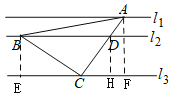
作AF⊥![]() ,BE⊥
,BE⊥![]() ,证明△ACF≌△CBE,求出CE,根据勾股定理求出BC、AC,作DH⊥
,证明△ACF≌△CBE,求出CE,根据勾股定理求出BC、AC,作DH⊥![]() ,根据DH∥AF证明△CDH∽△CAF,求出CD,再根据勾股定理求出BD.
,根据DH∥AF证明△CDH∽△CAF,求出CD,再根据勾股定理求出BD.
如图,作AF⊥![]() ,BE⊥
,BE⊥![]() ,则∠AFC=BEC=90°,
,则∠AFC=BEC=90°,
由题意得BE=3,AF=2+3=5,
∵△![]() 是等腰直角三角形,
是等腰直角三角形,![]() 90°,
90°,
∴AC=BC,∠BCE+∠ACF=90°,
∵∠BCE+∠CBE=90°,
∴∠ACF=∠CBE,
∴△ACF≌△CBE,
∴CE=AF=5,CF=BE=3,
∴![]() ,
,
作DH⊥![]() ,
,
∴DH∥AF
∴△CDH∽△CAF,
∴![]() ,
,
∴ ![]() ,
,
∴CD=![]() ,
,
∴BD=![]()
![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目