题目内容
【题目】如图,等腰三角形 ABC 中,AC=BC=13,AB=10.以 BC 为直径作⊙O 交 AB 于点 D,交 AC 于点 G,DF⊥AC,垂足为 F,交 CB 的延长线于点 E.
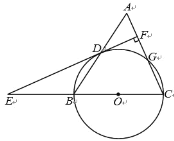
(1)求证:直线 EF 是⊙O 的切线;
(2)求 sin∠E 的值.
【答案】(1)见解析(2)![]()
【解析】
(1)求证直线EF是⊙O的切线,只要连接OD证明OD⊥EF即可;
(2)根据∠E=∠CBG,可以把求sin∠E的值得问题转化为求sin∠CBG,进而转化为求Rt△BCG中,两边的比的问题.
(1)证明:方法1:连接OD、CD.
∵BC是直径,
∴CD⊥AB.
∵AC=BC.
∴D是AB的中点.
∵O为CB的中点,
∴OD∥AC.
∵DF⊥AC,
∴OD⊥EF.
∴EF是O的切线.
方法2:∵AC=BC,
∴∠A=∠ABC,
∵OB=OD,
∴∠DBO=∠BDO,
∵∠A+∠ADF=90°
∴∠EDB+∠BDO=∠A+∠ADF=90°.
即∠EDO=90°,
∴OD⊥ED
∴EF是O的切线.
(2)解:连BG.
∵BC是直径,
∴∠BDC=90°.
∵AC=BC=13,AB=10
∴AD=![]() AB=5
AB=5
∴CD=![]()
∵ABCD=2S△ABC=ACBG,
∴BG=![]() =
=![]() .
.
∴CG=![]() .
.
∵BG⊥AC,DF⊥AC,
∴BG∥EF.
∴∠E=∠CBG,
∴sin∠E=sin∠CBG= =
=![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
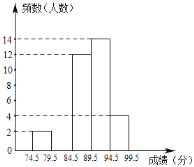
口算心算速算应用题系列答案【题目】为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
分数段 | 频数 | 频率 |
74.5~79.5 | 2 | 0.05 |
79.5~84.5 | m | 0.2 |
84.5~89.5 | 12 | 0.3 |
89.5~94.5 | 14 | n |
94.5~99.5 | 4 | 0.1 |
(1)表中m=__________,n=____________;
(2)请在图中补全频数直方图;
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在_________分数段内;
(4)选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.
【题目】参照学习函数的过程与方法,探究函数![]()
![]() 的图象与性质列表:
的图象与性质列表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
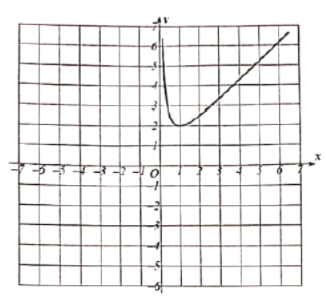
(1)请补全函数图象:
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,y随x的增大而_________;(填“增大”或“减小”)
时,y随x的增大而_________;(填“增大”或“减小”)
②图象关于点__________中心对称.(填点的坐标)
③当![]() 时,
时,![]() 的最小值是_________.
的最小值是_________.
(3)结合函数图象,当![]() 时,求x的取值范围.
时,求x的取值范围.