题目内容
【题目】(1)问题发现
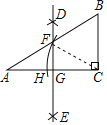
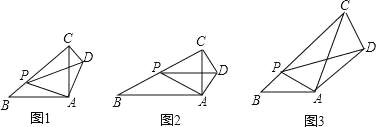
如图1,在Rt△ABC中,∠A=90°,![]() =1,点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接 CD.
=1,点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接 CD.
(1)①求![]() 的值;②求∠ACD的度数.
的值;②求∠ACD的度数.
(2)拓展探究
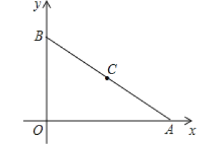
如图 2,在Rt△ABC中,∠A=90°,![]() =k.点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接CD,请判断∠ACD与∠B 的数量关系以及PB与CD之间的数量关系,并说明理由.
=k.点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接CD,请判断∠ACD与∠B 的数量关系以及PB与CD之间的数量关系,并说明理由.
(3)解决问题
如图 3,在△ABC中,∠B=45°,AB=4![]() ,BC=12,P 是边BC上一动点(不与点B重合),∠PAD=∠BAC,∠APD=∠B,连接CD.若 PA=5,请直接写出CD的长.
,BC=12,P 是边BC上一动点(不与点B重合),∠PAD=∠BAC,∠APD=∠B,连接CD.若 PA=5,请直接写出CD的长.
【答案】(1)1,45°;(2)∠ACD=∠B,![]() =k;(3)
=k;(3)![]() .
.
【解析】
(1)根据已知条件推出△ABP≌△ACD,根据全等三角形的性质得到PB=CD,∠ACD=∠B=45°,于是得到 ![]()
![]() 根据已知条件得到△ABC∽△APD,由相似三角形的性质得到
根据已知条件得到△ABC∽△APD,由相似三角形的性质得到![]() ,得到 ABP∽△CAD,根据相似三角形的性质得到结论;
,得到 ABP∽△CAD,根据相似三角形的性质得到结论;
![]() 过A作AH⊥BC 于 H,得到△ABH 是等腰直角三角形,求得 AH=BH=4, 根据勾股定理得到
过A作AH⊥BC 于 H,得到△ABH 是等腰直角三角形,求得 AH=BH=4, 根据勾股定理得到![]() 根据相似三角形的性质得到
根据相似三角形的性质得到 ![]() ,推出△ABP∽△CAD,根据相似三角形的性质即可得到结论.
,推出△ABP∽△CAD,根据相似三角形的性质即可得到结论.
(1)∵∠A=90°,
![]()
∴AB=AC,
∴∠B=45°,
∵∠PAD=90°,∠APD=∠B=45°,
∴AP=AD,
∴∠BAP=∠CAD,
在△ABP 与△ACD 中,
AB=AC, ∠BAP=∠CAD,AP=AD,
∴△ABP≌△ACD,
∴PB=CD,∠ACD=∠B=45°,
∴![]() =1,
=1,
(2)![]()
∵∠BAC=∠PAD=90°,∠B=∠APD,
∴△ABC∽△APD,
![]()
∵∠BAP+∠PAC=∠PAC+∠CAD=90°,
∴∠BAP=∠CAD,
∴△ABP∽△CAD,
∴∠ACD=∠B,
![]()
(3)过 A 作 AH⊥BC 于 H,
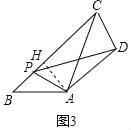
∵∠B=45°,
∴△ABH 是等腰直角三角形,
∵![]()
∴AH=BH=4,
∵BC=12,
∴CH=8,
∴![]()
∴PH=![]() =3,
=3,
∴PB=1,
∵∠BAC=∠PAD=,∠B=∠APD,
∴△ABC∽△APD,
∴![]() ,
,
∵∠BAP+∠PAC=∠PAC+∠CAD,
∴∠BAP=∠CAD,
∴△ABP∽△CAD,
∴![]() 即
即![]()
∴![]()
过 A 作 AH⊥BC 于 H,
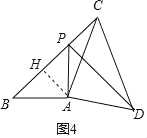
∵∠B=45°,
∴△ABH 是等腰直角三角形,
∵![]()
∴AH=BH=4,
∵BC=12,
∴CH=8,
∴![]()
∴PH=![]() =3,
=3,
∴PB=7,
∵∠BAC=∠PAD=,∠B=∠APD,
∴△ABC∽△APD,
∴![]() ,
,
∵∠BAP+∠PAC=∠PAC+∠CAD,
∴∠BAP=∠CAD,
∴△ABP∽△CAD,
∴![]() 即
即![]()
∴![]()