题目内容
【题目】如图所示,![]() 的直径
的直径![]() 为
为![]() ,弦
,弦![]() 为
为![]() ,
,![]() 的平分线交
的平分线交![]() 于E,且
于E,且![]() .
.
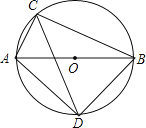
(1)求![]() ,
,![]() ,
,![]() 的长
的长
(2)图中还有一条线段![]() 的长是否能确定,若能求出
的长是否能确定,若能求出![]() 的长。
的长。
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)先根据直径所对的角是90°,判断出△ABC和△ABD是直角三角形,根据圆周角∠ACB的平分线交⊙O于D,判断出△ADB为等腰直角三角形,然后根据勾股定理求出具体值.
(2)过E作EF⊥AC于F,EG⊥BC于G,F,G是垂足,则四边形CFEG是正方形,设EF=EG=x,由三角形面积公式可求出x的值,及CE的值,根据△ADE∽△CBE,根据相似比可求出DE的长,进而求出CD的长.
(1)∵AB是直径
∴∠ACB=∠ADB=90°
在Rt△ABC中,AB2=AC2+BC2,AB=10cm,AC=6cm
∴BC2=AB2-AC2=102-62=64
∴BC=![]() =8(cm)
=8(cm)
又∵CD平分∠ACB,
∴弧AD=弧BD,
∴AD=BD,
又∵在Rt△ABD中,AD2+BD2=AB2
∴AD2+BD2=102
∴AD=BD=![]() =5
=5![]() (cm).
(cm).
(2)过E作EF⊥AC于F,EG⊥BC于G,F,G是垂足,则四边形CFEG是正方形,
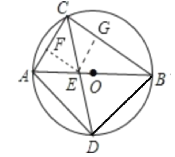
设EF=EG=x,
∴![]() ACx+
ACx+![]() BCx=
BCx=![]() ACBC
ACBC
∴![]() ×6x+
×6x+![]() ×8×x=
×8×x=![]() ×6×8
×6×8
∴x=![]() ,
,
∴CE=![]() x=
x=![]() ,
,
∵∠DAB=∠DCB,
∵△ADE∽△CBE
∴DE:BE=AE:CE=AD:BC
∴DE:BE=AE: ![]() =5
=5![]() :8
:8
∴AE=![]() ,BE=ABAE=10
,BE=ABAE=10![]() =
=![]()
∴DE=![]()
∴CD=CE+DE=![]() +
+![]() =7
=7![]() (cm).
(cm).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目