题目内容
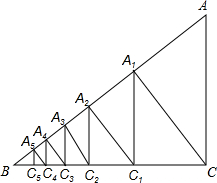 如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=8,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直作下去,得到了一组线段CA1,A1C1,C1A2,A2C2,…,AnCn,则A1C1=________,AnCn=________.
如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=8,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直作下去,得到了一组线段CA1,A1C1,C1A2,A2C2,…,AnCn,则A1C1=________,AnCn=________.


分析:首先由Rt△ABC中,∠ACB=90°,AC=6,BC=8,利用勾股定理即可求得AB的长,易证得△CA1B∽△ACB,然后由相似三角形的对应边成比例,求得A1C的值,同理可求得:A1C1,A2C1,A2C2的值,则可得规律:AnCn=6×(
 )2n.
)2n.解答:∵Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB=
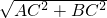 =10,
=10,∵CA1⊥AB,
∴∠CA1B=∠ACB=90°,
∵∠B是公共角,
∴△CA1B∽△ACB,
∴
 ,
,即
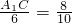 ,
,即A1C=
 AC=6×
AC=6× ,
,同理可得:A1C1=
 A1C=6×(
A1C=6×( )2=6×(
)2=6×( )2×1,
)2×1,A2C1=
 A1C1=6×(
A1C1=6×( )3,
)3,A2C2=
 A2C1=6×(
A2C1=6×( )4=6×(
)4=6×( )2×2,
)2×2,可得规律为:AnCn=6×(
 )2n.
)2n.故答案为:6×(
 )2,6×(
)2,6×( )2n.
)2n.点评:此题考查了相似三角形的判定与性质以及勾股定理.此题属于规律性题目,难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
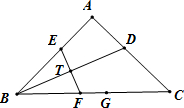 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG. E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE.
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF. 如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P. 如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为
如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为