Question

已知：如图一次函数y=x﹣3的图象与x轴、y轴分别交于A、B两点，过点C（4，0）作AB的垂线交AB于点E，交y轴于点D，求点D、E的坐标．

Answer 1

点D的坐标为（0，8）；点E的坐标为（，﹣）．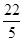

解析试题分析： 先求出点A坐标为（6，0），点B坐标为（0，﹣3），由于DE⊥AB，则∠AEC=90°，利用等角的余角相等得到∠ODC=∠EAC，易证得Rt△ODC∽Rt△OAB，得到OD：OA=OC：OB，即OD：6=4：3，
可求出OD=8，得到点D的坐标为（0，8）；然后利用待定系数法求出直线CD的解析式为y=﹣2x+8，再解由y=x﹣3和y=﹣2x+8的方程组即可得到点E坐标．
试题解析：对于y=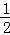x﹣3，令x=0，则y=﹣3；令y=0，x=6，
∴点A坐标为（6，0），点B坐标为（0，﹣3），
∵DE⊥AB，
∴∠AEC=90°，
∴∠ODC=∠EAC，
∴Rt△ODC∽Rt△OAB，
∴OD：OA=OC：OB，即OD：6=4：3，
∴OD=8，
∴点D的坐标为（0，8）；
设过CD的直线解析式为y=kx+8，将C（4，0）代入得0=4k+8，解得k=﹣2，
∴直线CD的解析式为y=﹣2x+8，
解方程组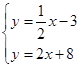得．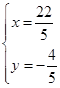
∴点E的坐标为（，﹣）．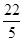
考点：两条直线相交或平行问题．