题目内容
在平面直角坐标系中,矩形ABCD的边AB在x轴上,点A、B的横坐标分别为a+2与2a﹣5,且关于y轴对称,BC的长为3,且点C在第三象限.
(1)求顶点A、C的坐标;
(2)若y=kx+b是经过点B,且与AC平行的一条直线,试确定它的解析式.
(1)A(3,0),C(﹣3,﹣3);(2)
解析试题分析:(1)根据关于y轴对称的点的坐标特征得到a+2+2a﹣5=0,解得a=1,则得到A点坐标为(3,0),B定坐标为(﹣3,0),然后利用矩形的性质和BC=3可得到C点坐标;(2)先利用待定系数法确定直线AC的解析式,然后利用一次函数图象与几何变换求解.
试题解析:(1)∵点A与点B关于y轴对称,
∴a+2+2a﹣5=0,解得a=1,
∴A点坐标为(3,0),B定坐标为(﹣3,0),
∵矩形ABCD的边BC=3,
∴C点坐标为(﹣3,﹣3);
(2)设直线AC的解析式为y=mx+n,
把A(3,0)、(﹣3,﹣3)代入得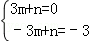 ,
,
解得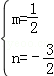 ,
,
∴直线AC的解析式为 ,
,
∵把直线AC向上平移3个单位得到过B点的直线,
∴经过点B,且与AC平行的直线解析式为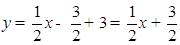 .
.
考点:1.待定系数法求一次函数解析式;2.一次函数图象与几何变换

练习册系列答案
相关题目
如表,给出A、B两种上网宽带的收费方式:
| 收费方式 | 月使用费/元 | 包月上网时间/小时 | 超时费/(元/分) |
| A | 30 | 20 | 0.05 |
| B | 60 | 不限时 | |
假设月上网时间为x小时,方式A、B的收费方式分别是yA(元)、yB(元).
(1)请写出yA、yB分别与x的函数关系式,并写出自变量的范围(注意结果要化简);
(2)在给出的坐标系中画出这两个函数的图象;
(3)结合图象与解析式,填空:
当上网时间x的取值范围是 _________ 时,选择方式A省钱;
当上网时间x的取值范围是 _________ 时,选择方式B省钱.

 分别交x轴、y轴于A、B两点,线段AB的垂直平分线分别交x轴于点.求点C的坐标并求△ABC的面积.
分别交x轴、y轴于A、B两点,线段AB的垂直平分线分别交x轴于点.求点C的坐标并求△ABC的面积.

 x﹣3的图象与x轴、y轴分别交于A、B两点,过点C(4,0)作AB的垂线交AB于点E,交y轴于点D,求点D、E的坐标.
x﹣3的图象与x轴、y轴分别交于A、B两点,过点C(4,0)作AB的垂线交AB于点E,交y轴于点D,求点D、E的坐标.

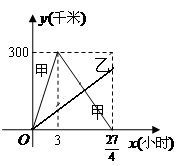
 两地同时出发相向而行,其中甲到
两地同时出发相向而行,其中甲到 地后立即返回,下图是它们离各自出发地的距离
地后立即返回,下图是它们离各自出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象.
(小时)之间的函数图象. 小时,求乙车离出发地的距离
小时,求乙车离出发地的距离