题目内容
如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y= (x>0)的图象经过矩形的对称中心E,且与边BC交于点 D.
(x>0)的图象经过矩形的对称中心E,且与边BC交于点 D.
(1)求反比例函数的解析式和点D的坐标;
(2)若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,求此直线的解析式.
(1)反比例函数解析式为y=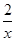 ,点D的坐标为(1,2);
,点D的坐标为(1,2);
(2)直线的解析式为y=﹣2x+4或y=﹣ x+
x+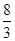 .
.
解析试题分析:(1)根据中心对称求出点E的坐标,再代入反比例函数解析式求出k,然后根据点D的纵坐标与点B的纵坐标相等代入求解即可得到点D的坐标;
(2)设直线与x轴的交点为F,根据点D的坐标求出CD,再根据梯形的面积分两种情况求出OF的长,然后写出点F的坐标,再利用待定系数法求一次函数解析式求出直线解析式即可.
试题解析:(1)∵矩形OABC的顶点B的坐标是(4,2),E是矩形ABCD的对称中心,
∴点E的坐标为(2,1),
代入反比例函数解析式得,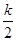 =1,
=1,
解得k=2,
∴反比例函数解析式为y=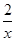 ,
,
∵点D在边BC上,
∴点D的纵坐标为2,
∴y=2时,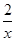 =2,
=2,
解得x=1,
∴点D的坐标为(1,2);
(2)如图,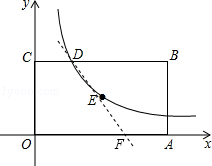
设直线与x轴的交点为F,
矩形OABC的面积=4×2=8,
∵矩形OABC的面积分成3:5的两部分,
∴梯形OFDC的面积为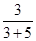 ×8=3,
×8=3,
或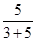 ×8=5,
×8=5,
∵点D的坐标为(1,2),
∴若 (1+OF)×2=3,
(1+OF)×2=3,
解得OF=2,
此时点F的坐标为(2,0),
若 (1+OF)×2=5,
(1+OF)×2=5,
解得OF=4,
此时点F的坐标为(4,0),与点A重合,
当D(1,2),F(2,0)时,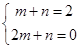 ,
,
解得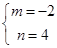 ,
,
此时,直线解析式为y=﹣2x+4,
当D(1,2),F(4,0)时,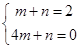 ,
,
解得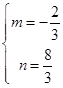 ,
,
此时,直线解析式为y=﹣ x+
x+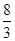 ,
,
综上所述,直线的解析式为y=﹣2x+4或y=﹣ x+
x+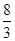 .
.
考点:1.矩形的性质2.待定系数法求一次函数解析式3.待定系数法求反比例函数解析式.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案如表,给出A、B两种上网宽带的收费方式:
| 收费方式 | 月使用费/元 | 包月上网时间/小时 | 超时费/(元/分) |
| A | 30 | 20 | 0.05 |
| B | 60 | 不限时 | |
假设月上网时间为x小时,方式A、B的收费方式分别是yA(元)、yB(元).
(1)请写出yA、yB分别与x的函数关系式,并写出自变量的范围(注意结果要化简);
(2)在给出的坐标系中画出这两个函数的图象;
(3)结合图象与解析式,填空:
当上网时间x的取值范围是 _________ 时,选择方式A省钱;
当上网时间x的取值范围是 _________ 时,选择方式B省钱.





 的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数
的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数
 的图象相交于点A(a,1),求直线l的解析式.
的图象相交于点A(a,1),求直线l的解析式. 的图象与反比例函数
的图象与反比例函数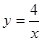 的图象交于点
的图象交于点 ,与
,与 轴交于点
轴交于点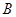 .
.