题目内容
【题目】为增强学生体质，某中学在体育课中加强了学生的长跑训练．在一次男子1000米耐力测试中，小明和小亮同时起跑，同时到达终点；所跑的路程S（米）与所用的时间t（秒）之间的函数图象如图所示：
（1）当80≤t≤180时，求小明所跑的路程S（米）与所用的时间t（秒）之间的函数表达式；
（2）求他们第一次相遇的时间是起跑后的第几秒？
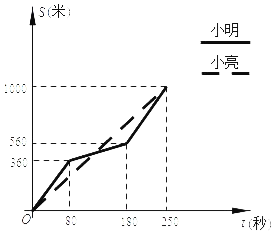
【答案】（1）当80≤t≤180时，小明所跑的路程S（米）与所用的时间t（秒）之间的函数表达式为y1＝2x+200；（2）他们第一次相遇的时间是起跑后的第100秒
【解析】
（1）用待定系数法求小明所跑的路程S（米）与所用的时间t（秒）之间的函数表达式；
（2）用待定系数法求小亮所跑的路程S（米）与所用的时间t（秒）之间的函数表达式，然后与（1）的表达式联立方程组，解方程组就可以求出第一次相遇时间．
（1）设当80≤t≤180时，小明所跑的路程S（米）与所用的时间t（秒）之间的函数表达式为y1＝k1x+b，由题意，得
，
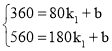解得：
，
∴当80≤t≤180时，小明所跑的路程S（米）与所用的时间t（秒）之间的函数表达式为y1＝2x+200，
（2）设小亮所跑的路程S（米）与所用的时间t（秒）之间的函数表达式为y＝kx，
代入（250，1000）得1000＝250k，
解得k＝4，
故小亮所跑的路程S（米）与所用的时间t（秒）之间的函数表达式为y＝4x，
当y＝y1时，4x＝2x+200，
解得：x＝100．
所以他们第一次相遇的时间是起跑后的第100秒．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
