题目内容
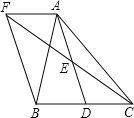
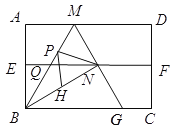
【题目】如图,在平面直角坐标系中,抛物线与矩形AOBC的边AC、BC分别交于点E,F,E(3,4),且F(8,![]() )为抛物线的顶点,将△CEF沿着EF翻折,点C恰好落在边OB上的点D处.
)为抛物线的顶点,将△CEF沿着EF翻折,点C恰好落在边OB上的点D处.
(1)求该抛物线的解析式;
(2)点P为线段ED上一动点,连接PF,当PF平分∠EFD时,求PD的长度;
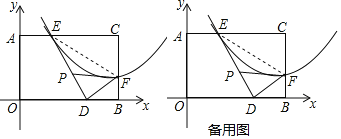
(3)四边形AODE以1个单位/秒的速度沿着x轴向右运动,当点E与点C重合时停止运动,设运动时间为t秒,运动后的四边形A′O′D′E′与△DEF重合部分的面积为S,请直接写出S与t的函数关系式.
【答案】(1)y=![]() (x-8)2+
(x-8)2+![]() ;(2)PD=
;(2)PD=![]() ;(3)S=
;(3)S=
【解析】
(1)设抛物线解析式为![]() ,把E(3,4)代入求出a=
,把E(3,4)代入求出a=![]() 即可;
即可;
(2)由折叠的性质得:DF=CF,∠EDF=∠C=90°,DE=CE=5,作EG⊥OB于G,则EG=OA=4,OG=AE=3,由勾股定理得出![]() ,得出BD=2,设DF=CF=x,则BF=4-x,在Rt△BDF中,由勾股定理得出方程,解方程得出DF=CF=
,得出BD=2,设DF=CF=x,则BF=4-x,在Rt△BDF中,由勾股定理得出方程,解方程得出DF=CF=![]() ,由勾股定理求出
,由勾股定理求出![]() ,作PH⊥EF于H,由角平分线性质得出PH=PD,证出△PEH∽△FED,得出
,作PH⊥EF于H,由角平分线性质得出PH=PD,证出△PEH∽△FED,得出![]() ,即可得出结果;
,即可得出结果;
(3)分三种情况:当0≤t≤3时,此时重合部分为一个梯形;当![]() 时,此时D′E′与DF的交点仍然在线段DF上,重合部分为一个梯形面积减去一个三角形的面积;当
时,此时D′E′与DF的交点仍然在线段DF上,重合部分为一个梯形面积减去一个三角形的面积;当![]() 时,重合部分为△DEF的面积减去一个三角形的面积.
时,重合部分为△DEF的面积减去一个三角形的面积.
解:(1)∵F(8,![]() )为抛物线的顶点,
)为抛物线的顶点,
∴设抛物线解析式为y=a(x-8)2+![]() ,把E(3,4)代入得:a(3-8)2+
,把E(3,4)代入得:a(3-8)2+![]() =4,解得:a=
=4,解得:a=![]() ,
,
∴该抛物线的解析式为:y=![]() (x-8)2+
(x-8)2+![]() ;
;
(2)∵四边形AOBC是矩形,
∴OB=AC=8,OA=BC=4,∠OBC=∠C=90°,
∵AE=3,∴CE=5,
由折叠的性质得:DF=CF,∠EDF=∠C=90°,DE=CE=5,
作EG⊥OB于G,则EG=OA=4,OG=AE=3,
∴DG=![]() =3,
=3,
∴BD=OB-OG-DG=2,
设DF=CF=x,则BF=4-x,在Rt△BDF中,由勾股定理得:
22+(4-x)2=x2,解得:x=![]() ,
,
∴DF=CF=![]() ,∴EF=
,∴EF=![]() =
=![]() =
=![]() ,
,
作PH⊥EF于H,
又∵PF平分∠EFD,∠PDF=90°,
∴PH=PD,
∵∠PHE=∠EDF=90°,∠PEH=∠FED,
∴△PEH∽△FED,
∴![]() =
=![]() ,即
,即![]() =
=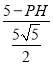 ,解得:PH=
,解得:PH=![]() ,∴PD=
,∴PD=![]() ;
;
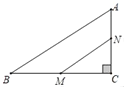
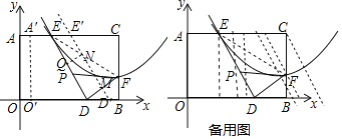
(3)分三种情况:如图所示:
①当0≤t≤3时,DD'=EE'=t,由(2)知,∠EDF=90°,由平移可知,D'E’⊥DF,
∴cos∠FDB=![]() =
=![]() =
=![]()
∴DM=![]() ,
,
设D'E'交EF于点M和点N,过点N作NQ⊥DE于点Q,则NQ=DM=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴EQ=![]() ,MN=DQ=5-
,MN=DQ=5-![]() ,
,
∴S=(5-![]() +5)
+5)![]() ÷2=
÷2=![]() +4t;
+4t;
②当3<t<![]() 时,D'E’与EF的交点在点F左侧,可知需要用梯形面积减去左边一个小三角形的面积,类比①可得:
时,D'E’与EF的交点在点F左侧,可知需要用梯形面积减去左边一个小三角形的面积,类比①可得:
S=![]() +4t-(
+4t-(![]() )=
)=![]()
③当![]() 时,S=
时,S=![]() -(
-(![]() )=
)=![]() -
-![]() +10
+10
故S与t的函数关系式为:
S=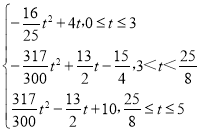

 一课一练课时达标系列答案
一课一练课时达标系列答案【题目】赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,全校同时默写50首古诗词,每正确默写出一首古诗词得2分,结果有500名进入决赛,从这500名的学生中随机抽取50名学生进行成绩分析,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:(最高分98分):
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
Ⅰ.第3组的具体分数为:70,70,70,72,72,74,74,74,76,76,78,78,78,78
Ⅱ.50人得分平均数、中位数、众数如表:
平均数 | 中位数 | 众数 | |
得分(分) | m | n |
请结合图表数据信息完成下列各题:
(1)填空a= ,m= ;
(2)将频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,估计进入决赛的本次测试为的优秀的学生有多少?