题目内容
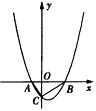
【题目】如图,二次函数y=x2+px+q(p<0)的图象与x轴交于A、B两点,与y轴交于点C(0,-1),△ABC的面积为![]() 。
。
(1)求该二次函数的关系式;
(2)过y轴上的一点M(0,m)作y轴的垂线,若该垂线与△ABC的外接圆有公共点,求m的取值范围;
(3)在该二次函数的图象上是否存在点D,使四边形ACBD为直角梯形?若存在,求出点D的坐标;若不存在,请说明理由。
【答案】(1)y=![]() ;(2)-
;(2)- ![]() ≤m≤
≤m≤![]() ;(3) (
;(3) (![]() ,
, ![]() 或(-
或(-![]() ,9)
,9)
【解析】试题分析:(1)由△ABC的面积为![]() ,可得AB×OC=
,可得AB×OC=![]() ,又二次函数y=x2+px+q(p<0)的图象与x轴交于A、B两点,与y轴交于点C(0,-1)可求得该二次函数的关系式;
,又二次函数y=x2+px+q(p<0)的图象与x轴交于A、B两点,与y轴交于点C(0,-1)可求得该二次函数的关系式;
(2)根据直线与圆的位置的位置关系确定m的取值范围.
(3)四边形ABCD为直角梯形,要分类讨论,即究竟那条边为底.可以分别以AC、BC为底进行讨论.
试题解析:
(1)由点C的坐标为(0,-1),得OC=1,
又∵△ABC的面积为![]() ,
,
∴![]() ,即
,即![]() ,
,
由抛物线与y轴交于(0,-1),
得y=x2+px+g(p<0)中的q=-1,
则当y=0时,0=x2+px-1,设它的两个根为x1、x2,
则x1+x2=-p,x1x2=-1,且A、B两点的坐标为(x1,0)、(x2,0),
由直角坐标系上两点间的距离公式可得x2-x1=AB=![]() ,
,
∴![]() ,
,
∴x12+x22-2x1x2=![]() ,
,
∴x12+x22+2x1x2-4x1x2=![]() ,
,
∴(x1+x2)2-4x1x2=![]() ,即p2+4=
,即p2+4=![]() ,解得
,解得![]() ,
,
∵p<0,∴p=![]() ,
,
∴该抛物线的关系式为![]() ;
;
(2)设△ABC的外接圆交y轴于另一点D,如图
由![]() 得x1=2,
得x1=2,![]() ,
,
∴![]() ,
,
连接AD,

在△ABC的外接圆中,
∵![]() ,
,
∴∠ADC=∠ABC,∠DAB=∠DCB,
∴△AOD∽△COB,
∴![]() ,
,
∴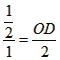 ,
,
∴DO=1,
∴CO=DO=1,
又∵AB⊥CD,
∴AB过△ABC外接圆的圆心,即AB为△ABC外接圆的直径,
∴△ABC外接圆的直径为![]() ,
,
∴直线![]() 与△ABC的外接圆相切,
与△ABC的外接圆相切,
∴![]() ;
;
(3)存在
∵AB是△ABC外接圆的直径,
∴∠ACB=90°,这时抛物线上必有点D,且当AD∥BC或BD∥AC时使四边形ACBD为直角梯形,
当AD∥BC时,可求得直线BC的关系式为![]() ,
,
∴直线AD的关系式为![]() ,
,
则它与抛物线![]() 的交点坐标为
的交点坐标为![]() ,
,
此时点D的坐标为![]() ,
,
当BD∥AC时,可求直线AC的关系式为y=-2x-1,
∴直线BD的关系式为y=-2x+4,
则它与抛物线![]() 的交点坐标为
的交点坐标为![]() ,
,
此时点D的坐标为![]() ,
,
∴当点D在![]() 或
或![]() 的位置时,四边形ACBD为直角梯形。
的位置时,四边形ACBD为直角梯形。

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
