��Ŀ����
����Ŀ������ƽ��ֱ���ϸ���n���㣬����n�Ե㰴���µĹ��������߶Σ�
��ƽ����֮��ĵ������߶�ʱ�������й�ͬ�Ķ˵㣬���������������㣻
��������Ҫ����߶α���ȫ��������
ͼ1չʾ�˵�n=1ʱ���������ʱͼ�������εĸ���Ϊ0��
ͼ2չʾ�˵�n=2ʱ��һ���������ʱͼ�������εĸ���Ϊ2��
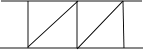
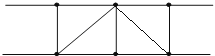
��1����n=3ʱ������ͼ3�л���ʹ�����θ������ٵ�ͼ�Σ���ʱͼ�������εĸ���Ϊ__________����
��2���Բ��뵱n�Ե�ʱ��������������ͼ���У������ж��ٸ������Σ�
��3����n=2006ʱ��������������ͼ���У������ж��ٸ������Σ�

���𰸡���1��4��2��n��2��n-1����3��4010
�������������������1����ϸ�������⣬ȷ����ͼ�μ��ɵõ������
��2�������ɵã���![]() ʱͼ�������εĸ���Ϊ0����
ʱͼ�������εĸ���Ϊ0����![]() ����
����![]() ʱͼ�������εĸ���Ϊ2����
ʱͼ�������εĸ���Ϊ2����![]() ����������������ɼ��ɵõ�����n�Ե�ʱ�����ٿ��Ի��������ε���Ŀ��
����������������ɼ��ɵõ�����n�Ե�ʱ�����ٿ��Ի��������ε���Ŀ��
��3����![]() ���루2���еõ��Ĺ��ɼ��ɵõ������
���루2���еõ��Ĺ��ɼ��ɵõ������
��1����![]() ʱ����ͼ��ʾ����ʱͼ�������εĸ���Ϊ 4 ����
ʱ����ͼ��ʾ����ʱͼ�������εĸ���Ϊ 4 ����
��2����![]() ʱͼ�������εĸ���Ϊ0����
ʱͼ�������εĸ���Ϊ0����![]() ��
��
��![]() ʱͼ�������εĸ���Ϊ2����
ʱͼ�������εĸ���Ϊ2����![]() ��
��
����
����![]() �Ե�ʱ��������������ͼ���У�������
�Ե�ʱ��������������ͼ���У�������![]() �������Σ�
��������
��3����![]() ʱ��
ʱ��![]() ��������
��������
�𣺵�![]() ʱ��������������ͼ���У�������4024��������.
ʱ��������������ͼ���У�������4024��������.