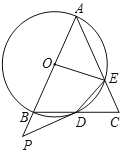题目内容
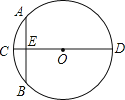
【题目】“圆材埋壁”是我国古代数一学著作《九章算术》中的一个问题.“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表达是:如图所示,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=1尺,则直径CD长为_____寸.
【答案】26
【解析】
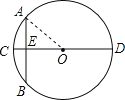
连接OA,设OA=r,则OE=r-CE=r-1,再根据垂径定理求出AE的长,在Rt△OAE中根据勾股定理求出r的值,进而得出结论.
解:连接OA,设OA=r,则OE=r﹣CE=r﹣1,
∵AB⊥CD,AB=1尺,
∴AE=![]() AB=5寸,
AB=5寸,
在Rt△OAE中,
OA2=AE2+OE2,即r2=52+(r﹣1)2,
解得r=13(寸).
∴CD=2r=26寸.
故答案为:26.

练习册系列答案
相关题目
【题目】主题班会课上,王老师出示了如图一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟,根据同学们的选择情况,小明绘制了如图两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
观点 | 频数 | 频率 |
A | a | 0.2 |
B | 12 | 0.24 |
C | 8 | b |
D | 20 | 0.4 |

(1)参加本次讨论的学生共有 人;
(2)表中a= ,b= ;
(3)将条形统计图补充完整;
(4)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.