题目内容
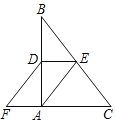
【题目】如图,在Rt△ABC中∠BAC=90°,D,E分别是AB,BC的中点,F在CA的延长线上∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为_____.
【答案】16
【解析】
根据勾股定理先求出BC的长,再根据三角形中位线定理和直角三角形的性质求出DE和AE的长,进而由已知可判定四边形AEDF是平行四边形,从而求得其周长.
解:∵在Rt△ABC中,AC=6,AB=8,
∴BC=10,
∵E是BC的中点,
∴AE=BE=CE=![]() BC=5,
BC=5,
∴∠BAE=∠B,
∵∠FDA=∠B,
∴∠FDA=∠BAE,
∴DF∥AE,
∵D、E分别是AB、BC的中点,
∴DE∥AC,DE=![]() AC=3,
AC=3,
∴四边形AEDF是平行四边形,
∴四边形AEDF的周长=2×(3+5)=16.
故答案为:16.

练习册系列答案
相关题目