题目内容
【题目】已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.
(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC于点F.求证:BF+EF=DE;
(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由.

【答案】(1)证明见解析;(2) (1)中的结论不成立,有DE=BF﹣EF,理由见解析.
【解析】试题分析:(1)由Rt△ABC≌Rt△ADE得AC=AE,根据HL可证得Rt△ACF≌Rt△AEF,由BC=BF+CF代入可得结论;
(2)如图②,(1)中的结论不成立,有DE=BF-EF,同(1):证明Rt△ACF≌Rt△AEF,再由BC=BF-FC得出结论.
试题解析:(1)如图①,连接AF,
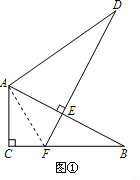
∵Rt△ABC≌Rt△ADE,
∴AC=AE,BC=DE,
∵∠ACB=∠AEF=90°,AF=AF,
∴Rt△ACF≌Rt△AEF,
∴CF=EF,
∴BF+EF=BF+CF=BC,
∴BF+EF=DE;
(2)如图②,(1)中的结论不成立,有DE=BF-EF,理由是:
连接AF,

∵Rt△ABC≌Rt△ADE,
∴AC=AE,BC=DE,
∵∠E=∠ACF=90°,AF=AF,
∴Rt△ACF≌Rt△AEF,
∴CF=EF,
∴DE=BC=BF-FC=BF-EF,
即DE=BF-EF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目