题目内容
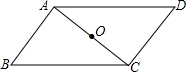
如图△ABC,AB=BC,将△ABC绕点A逆时针旋转一定的角度得到△AB′C′,当点C′恰好能落在BC的中点处时,B′C′与AB交于点F,若AC=2,则C′F的长为______.


∵AB=BC,
∴∠BAC=∠C,
∵△ABC绕点A逆时针旋转一定的角度得到△AB′C′,点C′恰好能落在BC的中点处,
∴AC=AC′,BC=B′C′,∠B=∠B′,
∴∠AC′C=∠C,
∴∠BAC=∠AC′C=∠C,
∴△ACC′∽△BAC,
∴AB:AC=AC:CC′,
∵AC=2,
∴2CC′:2=2:CC′,
∴CC′=
,
∴AB=BC=B′C′=B′A=2
,BC′=
,
∵∠B=∠B′,∠BFC′=∠B′FA,
∴△BFC′∽△∠B′FA,
∴BF:B′F=FC′:FA=BC′:B′A=
:2
=1:2,
设BF=x,FC′=y,则B′F=2x,FA=2y,
∵B′F+FC′=B′C′=2
,BF+FA=2
,
∴
,
解得
,
∴C′F的长为
.
故答案为
.
∴∠BAC=∠C,
∵△ABC绕点A逆时针旋转一定的角度得到△AB′C′,点C′恰好能落在BC的中点处,
∴AC=AC′,BC=B′C′,∠B=∠B′,
∴∠AC′C=∠C,
∴∠BAC=∠AC′C=∠C,
∴△ACC′∽△BAC,
∴AB:AC=AC:CC′,
∵AC=2,
∴2CC′:2=2:CC′,
∴CC′=
| 2 |
∴AB=BC=B′C′=B′A=2
| 2 |
| 2 |
∵∠B=∠B′,∠BFC′=∠B′FA,
∴△BFC′∽△∠B′FA,
∴BF:B′F=FC′:FA=BC′:B′A=
| 2 |
| 2 |
设BF=x,FC′=y,则B′F=2x,FA=2y,
∵B′F+FC′=B′C′=2
| 2 |
| 2 |
∴
|
解得
|
∴C′F的长为
2
| ||
| 3 |
故答案为
2
| ||
| 3 |

练习册系列答案
相关题目