题目内容
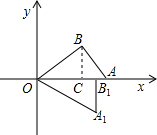
如图，平面直角坐标系中，∠ABO=90°，将直角△AOB绕O点顺时针旋转，使点B落在x轴上的点B1处，点A落在A1处，若B点的坐标为（
，
），则点A1的坐标是（ ）
| 16 |
| 5 |
| 12 |
| 5 |
| A．（3，-4） | B．（4，-3） | C．（5，-3） | D．（3，-5） |
作BC⊥OA于点C．
∵B点的坐标为（
，
），∴OC=
，BC=
．
∴根据勾股定理得OB=4；
根据射影定理得，OB2=OC•OA，
∴OA=5，∴AB=3．
∴OB1=4，A1B1=3．
∵A1在第四象限，
∴A1（4，-3）．
故选B．
∵B点的坐标为（
| 16 |
| 5 |
| 12 |
| 5 |
| 16 |
| 5 |
| 12 |
| 5 |
∴根据勾股定理得OB=4；
根据射影定理得，OB2=OC•OA，
∴OA=5，∴AB=3．
∴OB1=4，A1B1=3．
∵A1在第四象限，
∴A1（4，-3）．
故选B．
练习册系列答案
名校课堂系列答案
相关题目
