题目内容
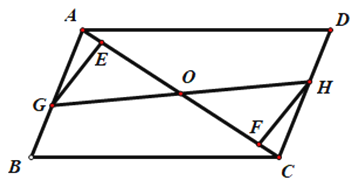
【题目】如图,在平行四边形ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.
(1)求证:EG//FH;
(2)GH、EF互相平分.
【答案】(1)见解析 (2)见解析
【解析】
(1)由平行四边形的性质得到AB平行CD,得到内错角∠GAO=∠FCH,根据AF=CE,同时减去EF可得AE=CF,根据SAS可证△ AGE≌△CHF,得到∠AEG=∠CFH,再由邻补角得到内错角相等,得到两线平行;
(2)连接FG、EH ,由(1)可证四边形EGFH是平行四边形即可得到结论.
在ABCD中,
∵AB∥CD,
∴∠GAE=∠HCF,
∵AF=CE,
∴AF-EF=CE=EF,
即;AE=CF,
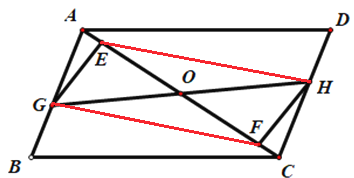
在△AGE与△CHF中,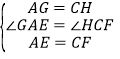 ,
,
∴△AGE≌△CHF(SAS),
∴∠AEG=∠CFH,
∴∠GEO=∠HFO,
∴EG∥FH;
(2)连接FG、EH
由(1)证得△AGE≌△CHF ,EG∥FH,
∴GE=HF,
∴四边形GFHE是平行四边形,
∴GH、EF互相平分.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案【题目】某乒乓球的质量检验结果如下:
抽取的乒乓球数n | 50 | 100 | 200 | 500 | 1000 | 1500 | 2000 |
优等品的频数m | 48 | 95 | 188 | x | 948 | 1426 | 1898 |
优等品的频率 | 0.960 | y | 0.940 | 0.944 | z | 0.951 | 0.949 |
(1)根据表中信息可得:x=______,y=______,z=______;
(2)从这批乒乓球中,任意抽取一只乒乓球是优等品的概率的估计值是多少?(精确到0.01).
【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备 | A型 | B型 |
价格(万元/台) | m | m-3 |
月处理污水量(吨/台) | 220 | 180 |
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.