题目内容
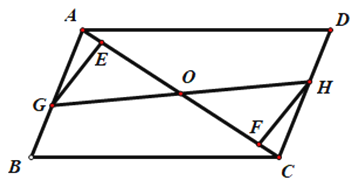
【题目】如图，在菱形ABCD中，AC、BD交于点O，AD＝15，AO＝12．动点P以每秒2个单位的速度从点A出发，沿AC向点C匀速运动．同时，动点Q以每秒1个单位的速度从点D出发，沿DB向点B匀速运动．当其中有一点列达终点时，另一点也停止运动，设运动的时间为t秒．
（1）求线段DO的长；
（2）设运动过程中△POQ两直角边的和为y，请求出y关于x的函数解析式；
（3）请直接写出点P在线段OC上，点Q在线段DO上运动时，△POQ面积的最大值，并写出此时的t值．
【答案】（1）9（2）见解析（3）当t＝
时，△POQ面积的最大值
【解析】
（1）根据菱形的对角线互相垂直平分的性质得到直角△AOD，在该直角三角形中利用勾股定理来求线段DO的长度；
（2）需要分类讨论：点P在线段OA上、点Q在线段OD上；点P在线段OC上，点Q在线段OD上；点P在线段OC上，点Q在线段OB上；
（3）由6＜t≤9时OP＝12﹣2t、OQ＝9﹣t可得△POQ的面积S＝
（9﹣t）（12﹣2t）＝﹣t2+15t﹣54＝﹣（t﹣）2+
，利用二次函数的性质求解可得．
（1）∵四边形ABCD是菱形，
∴AC⊥BD．
在Rt△AOD中，AD＝15，AO＝12
由勾股定理得：
OD＝
＝9．
（2）①当0≤t≤6时，OP＝12﹣2t，OQ＝9﹣t，则OP+OQ＝12﹣2t+9﹣t＝﹣3t+21
即：y＝﹣3t+21；
②当6＜t≤9时，OP＝2t﹣12，OQ＝9﹣t，则OP+OQ＝2t﹣12+9﹣t＝t﹣3
即：y＝t﹣3；
③当9＜t≤12时，OP＝2t﹣12，OQ＝t﹣9，则OP+OQ＝2t﹣12+t﹣9＝3t﹣21
即：y＝3t﹣21；
综上所述：y＝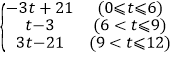
；
（3）如图，
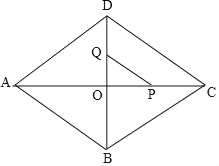
当6＜t≤9时，∵OP＝12﹣2t、OQ＝9﹣t，
∴△POQ的面积S＝（9﹣t）（12﹣2t）
＝﹣t2+15t﹣54
＝﹣（t﹣）2+，
∴当t＝时，△POQ面积的最大值．
