题目内容
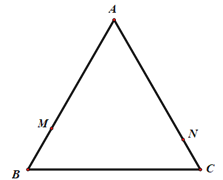
【题目】如图，等边△ABC的边长为8，动点M从点B出发，沿B→A→C→B的方向以每秒3个单位长度的速度运动，动点N从点C出发，沿C→A→B－C的方向以每秒2个单位长度的速度运动.
（1）若动点M、N同时出发，经过几秒第一次相遇？
（2）若动点M、N同时出发，且其中一点到达终点时，另一点即停止运动．在△ABC的边上是否存在一点D，使得以点A、M、N、D为顶点的四边形为平行四边形？若存在，求此时运动的时间
及点D的具体位置；若不存在，请说明理由.
【答案】（1）经过t=
s第一次相遇. （2）运动了
或
s时，A、M、N、D四点能够成平行四边形，此时点D在BC上，且BD=或
．
【解析】
（1）设经过t秒钟两点第一次相遇，然后根据点M运动的路程+点N运动的路程=AB+CA列方程求解即可；
（2）首先根据题意画出图形：如图②，当0≤t≤
时，AN+CN=MB+CN=8；当＜t≤4时，此时A、M、N三点在同一直线上，不能构成平行四边形；当4＜t≤
时，AN+NB=AN+AM=8；当＜t≤8时，△BNM为等边三角形，由BN=BM可求得t的值，可得此时M、N重合，不能构成平行四边形．．
（1）由题意得：3t+2t=16，解得：t=；
答：若动点M、N同时出发，经过t=s第一次相遇.
（2）①当0≤t≤时，点M、N、D的位置如图2所示：
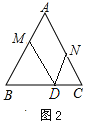
∵四边形ANDM为平行四边形，
∴DM=AN，DM∥AN．
∴∠MDB=∠C=60°
∵△ABC为等边三角形，
∴∠B=∠C=60°．
∴∠MDB =∠B．
∴MB=MD= AN
∴AN+CN=MB+CN=8，即：3t+2t=8，t=
，
此时点D在BC上，且BD=（或CD=），
②当＜t≤4时，此时A、M、N三点在同一直线上，不能构成平行四边形；
③4＜t≤时，点M、N、D的位置如图所1示：
∵四边形ANDM为平行四边形，
∴DN=AM，AM∥DN．
∴∠NDB=∠C=60°
∵△ABC为等边三角形，
∴∠B=∠C =60°．
∴∠NDB=∠B．
∴BN=ND= AM．
∴AN+NB=AN+AM=8，2t-8+3t-8=8，解得：t=，
此时点D在BC上，且BD=（或CD=），
④当＜t≤8时，点M、N、D的位置如图所3示：
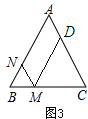
则BN=16-2t，BM=24-3t，
∵△ABC为等边三角形，
∴∠A=∠C=60°．
若MN∥AC,则∠BNM=∠A=60°, ∠BMN=∠C=60°
∴△BNM为等边三角形，
∴BN=BM，即：16-2t =24-3t，解得t=8，此时M、N重合，不能构成平行四边形．
答：运动了或s时，A、M、N、D四点能够成平行四边形，此时点D在BC上，且BD=或．
