题目内容
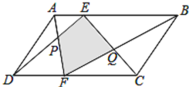
【题目】如图所示,E、F分别是□ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=2cm2,S△BQC=4cm2,则阴影部分的面积为( )
A. 6 cm2B. 8 cm2C. 10 cm2D. 12 cm2
【答案】A
【解析】
连接E、F两点,由三角形的面积公式我们可以推出S△EFC=S△BCF,S△EFD=S△ADF,所以S△EFG=S△BCQ,S△EFP=S△ADP,因此可以推出阴影部分的面积就是S△APD+S△BQC.
连接E、F两点,

∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△EFC的FC边上的高与△BCF的FC边上的高相等,
∴S△EFC=S△BCF,
∴S△EFQ=S△BCQ,
同理:S△EFD=S△ADF,
∴S△EFP=S△ADP,
∵S△APD=2cm2,S△BQC=4cm2,
∴S四边形EPFQ=6cm2,
故阴影部分的面积为6cm2.
故选A.

练习册系列答案
相关题目
【题目】某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价﹣进价),这两种服装的进价、标价如下表所示:
类型 价格 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)求这两种服装各购进的件数;
(2)如果A中服装按标价的8折出售,B中服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价售出少收入多少元?