题目内容
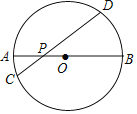
【题目】如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A. ![]() B. 2
B. 2![]() C. 2
C. 2![]() D. 8
D. 8
【答案】C
【解析】
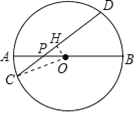
作OH⊥CD于H,连结OC,如图,根据垂径定理由OH⊥CD得到HC=HD,再利用AP=2,BP=6可计算出半径OA=4,则OP=OA-AP=2,接着在Rt△OPH中根据含30°的直角三角形的性质计算出OH=![]() OP=1,然后在Rt△OHC中利用勾股定理计算出CH=
OP=1,然后在Rt△OHC中利用勾股定理计算出CH=![]() ,所以CD=2CH=2
,所以CD=2CH=2![]() .
.
作OH⊥CD于H,连结OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=30°,
∴∠POH=30°,∴OH=![]() OP=1,
OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH=![]() ,
,
∴CD=2CH=2![]() .
.
故选C.

练习册系列答案
相关题目