题目内容
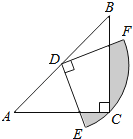
【题目】如图，在△ABC中，AB=AC, AD是∠BAC的平分线，AD⊥BC, CE⊥AB．CE交AD于点F，AE=CE.
(1)你能说明△AEF与△CEB全等吗？
(2)若AF=12cm，求CD的长．
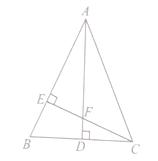
【答案】（1）证明见解析（2）6cm
【解析】（1）根据直角三角形两锐角互余可推得∠EAF =∠ECB，再结合AE =CE，∠AEF =∠CEB =90°，根据ASA即可得到△AEF≌△CEB；
（2）由△AEF≌△CEB可得BC=AF，再根据等腰三角形的“三线合一”的性质即可求得CD长.
（1）因为AD⊥BC，
所以∠B +∠BAD =90°.
因为CE⊥AB，
所以∠B +∠BCE =90°，
所以∠EAF =∠ECB，
在△AEF和△CEB中，
，
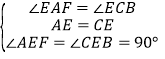所以△AEF≌△CEB（ASA）；
（2）因为△AEF ≌△CEB，
所以AF =BC，
因为AB =AC，AD⊥BC，
所以CD =BD =
BC，
所以CD=×12=6cm．
练习册系列答案
相关题目
