��Ŀ����
����Ŀ����ͼ1����֪�������µ�������y1=ax2��2ax+1����A��m��1������y�ύ�ڵ�C������ΪB����������y1�Ƶ�C��ת180���õ�������y2 �� ��A��B�Ķ�Ӧ��ֱ�Ϊ��D��E��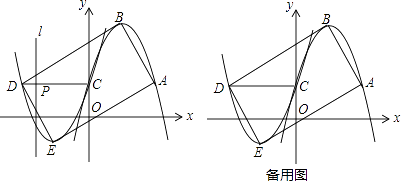
��1��ֱ��д����A��C��D�����ꣻ
��2�����ı���ABCD�Ǿ���ʱ����a��ֵ��������y2�Ľ���ʽ��
��3���ڣ�2���������£�����DC���߶�DC�ϵĶ���P�ӵ�D��������ÿ��1����λ���ȵ��ٶ��˶�����Cֹͣ���ڵ�P�˶��Ĺ����У�����P��ֱ��l��x�ᣬ������ABDE��ֱ��l�۵���������۵�����غϲ������ΪSƽ����λ����P���˶�ʱ��Ϊt�룬��S��t�ĺ�����ϵ��
���𰸡�
��1��
�⣺������ã�
��A��m��1������y1=ax2��2ax+1�ã�am2��2am+1=1��
��ã�m1=2��m2=0���ᣩ��
��A��2��1����C��0��1����D����2��1����
��2��
�⣺��ͼ1��
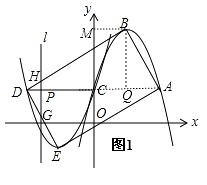
�ɣ�1��֪��B��1��1��a��������B��BM��y�ᣬ
���ı���ABDEΪ���Σ���BC=CD��
��BM2+CM2=BC2=CD2��
��12+����a��2=22��
��a= ![]()
![]() ��
��
��y1�����߿������£�
��a=�� ![]() ��
��
��y2��y1�Ƶ�C��ת180��õ�����E����1��1�� ![]() ����
����
����y2=a��x+1��2+1�� ![]() ����a=
����a= ![]() ��
��
��y2= ![]() x2+2
x2+2 ![]() x+1��
x+1��
��3��
�⣺��ͼ2��
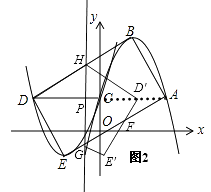
��0��t��1ʱ����DP=t������ֱ�ǡ�BQD��
��BQ= ![]() ��DQ=3����BD=2
��DQ=3����BD=2 ![]() ��
��
���BDQ=30�㣬
��PH= ![]() t��PG=
t��PG= ![]() t��
t��
��S= ![]() ��PE+PF����DP=
��PE+PF����DP= ![]() t2��
t2��
��ͼ2����1��t��2ʱ��EG=E��G= ![]() ��t��1����E��F=2��t��1����
��t��1����E��F=2��t��1����
S���غ�= ![]() ��t��1��2��
��t��1��2��
S=S1+S2��S���غ�= ![]() +
+ ![]() ��t��1����
��t��1���� ![]() ��t��1��2��
��t��1��2��
=�� ![]()
����������S= ![]() t2��0��t��1����S=��
t2��0��t��1����S=�� ![]() ��1��t��2����
��1��t��2����
�����������⿼���˶��κ��������ʣ���ת�����ʺ;��ζԽ��ߵ����ʣ��Լ����Ǻ���������ǵ�Ӧ�ã��ۺ��Խ�ǿ�����ڴ���֪���ھ����������DZ���Ĺؼ����������Լ�����εı߳����Խ�����ߵļнǣ��ó�30�㣬�Դ�Ϊͻ�ƿڣ�����Ҫ�ı߳���t��ʾ���ó�������ϵʽ�����Ȿ������˷������۵�˼�룬���ڶ��κ��������ý϶࣬Ӧ�������գ���1��ֱ�ӽ���A���������y1=ax2��2ax+1�ó�m��ֵ����Ϊ��ͼ���֪��A�ڵ�һ���ޣ�����m��0����m=2��д��A��C�����꣬��D���A���ڵ�C�Գƣ��ɴ�д����D�����ꣻ��2�����ݶ������깫ʽ�ó�������y1�Ķ���B�����꣬���ɾ��ζԽ��������ƽ�ֵã�BC=CD����ֱ�ǡ�BMC�У��ɹ��ɶ����з������a��ֵ�ó�������y1�Ľ���ʽ������ת�����ʵó�������y2�Ľ���ʽ����3��������������ۣ��ٵ�0��t��1ʱ��S=S��GHD=S��PDH+S��PDG �� �������߹���ֱ�������Σ����PG��PH�����������ʽ���㣻�ڵ�1��t��2ʱ��S=Sֱ��������+S������S���غ� �� ���ﲻ�غϵ�ͼ�ξ��ǡ�GE��F������30��Ǻ�60��ǵ�ֱ�������ε����ʽ��м���ó����ۣ�
�����㾫����ͨ��������ö��κ��������ʺ;��ε����ʣ����������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С�����ε��ĸ��Ƕ���ֱ�ǣ����εĶԽ�����ȼ����Խ����⣮