��Ŀ����
����Ŀ��(1)���������֣�
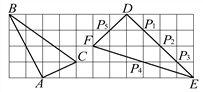
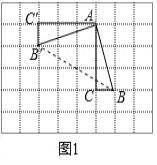
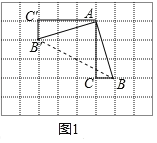
��ͼ 1���ڱ߳�Ϊ 1 ����λ���ȵ�С��������ɵ������У�ABC ������������ڸ���ϣ��ֽ�ABC �Ƶ� A ��˳ʱ�뷽����ת 90������ B �Ķ�Ӧ��Ϊ B������ C �Ķ�Ӧ��Ϊ C���� ���� BB������ͼ��ʾ���AB��B�� ��
��2����������⣩
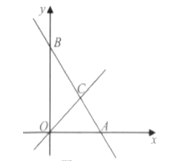
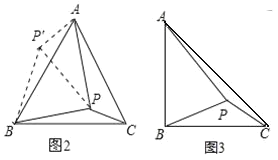
��ͼ 2���ڵȱ�ABC ����һ�� P���� PA��2��PB��![]() ��PC��1���������BPC �Ƶ� B ˳ʱ����ת 60���ó���ABP�������BPC �Ķ����� PP���ij���
��PC��1���������BPC �Ƶ� B ˳ʱ����ת 60���ó���ABP�������BPC �Ķ����� PP���ij���
��3����������ã�
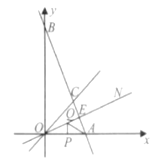
��ͼ 3������2���������ڵȱ�ABC ����һ�� P ��Ϊ���ڵ���ֱ�������� ABC ����һ��P������ BA=BC,PA��6��BP��4��PC��2�����BPC �Ķ���.
���𰸡���1����ͼ1��ʾ����������45�㣻��2����BPC��150�㣬PP�䣽![]() ����3����BPC��135��.
����3����BPC��135��.
��������
��1��������ת�ǣ���ת����ͼ�μ��ɣ�ֻҪ֤����ABB'�ǵ���ֱ�������μ��ɣ�
��2��������ת�����ʣ��ɵá�P'PB�ǵȱ������Σ��ɵȱ������ε����ʼ������PP'�ij�������PP'A����ֱ�������Σ��ɹ��ɶ������涨����֤�������ԡ�AP'B=150�㣬�Ӷ��ó����ۣ�
��3������BPC�Ƶ�B��ʱ����ת90��õ���AEB���루1�����ƣ��ɵã���EBP=��EBA+��ABP=��ABC=90�㣬�����BEP=45�㣬���ݹ��ɶ������涨�������AEP=90�㣬���ɵó����ۣ�
��ͼ1��ʾ������BB'������ABC�Ƶ�A��˳ʱ�뷽����ת90�㣬
��AB=AB'����B'AB=90�㣬���AB'B=45�㣮
�ʴ�Ϊ45�㣻
��2������ABC�ǵȱ������Σ�
���ABC=60����
����BPC�Ƶ�B˳ʱ����ת60���ó���ABP'����ͼ2��
��AP'=CP=1��BP'=BP=![]() ����PBC=��P'BA����AP'B=��BPC��
����PBC=��P'BA����AP'B=��BPC��
�ߡ�PBC+��ABP=��ABC=60����
���ABP'+��ABP=��ABC=60����
����BPP'�ǵȱ������Σ�
��PP'=![]() ����BP'P=60����
����BP'P=60����
��AP'=1��AP=2��
��AP'2+PP'2=12+��![]() ��2 =4��AP2=22=4��
��2 =4��AP2=22=4��
��AP'2+PP'2=AP2��
���AP'P=90��������PP'A��ֱ�������Σ�
���BPC=��AP'B=90��+60��=150����

��3����ͼ3������BPC�Ƶ�B��ʱ����ת90���õ���AEB��
�루1�����ƣ��ɵã�AE=PC=2��BE=BP=4����BPC=��AEB����ABE=��PBC�����EBP=��EBA+��ABP=��ABC=90����
���BEP=![]() ��180����90����=45����
��180����90����=45����
�ɹ��ɶ����ã�EP=![]() ��
��
��AE=2��AP=6��EP=![]() ��
��
��AE2+PE2=22+![]() 2=36 2=62=36��
2=36 2=62=36��
��AE2+PE2=AP2��
���AEP=90����
���BPC=��AEB=90��+45��=135����