题目内容
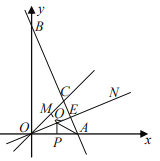
【题目】如下图,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC:y=x交于点C.
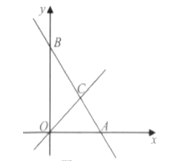
(1)若直线AB解析式为![]() .
.
①求点C的坐标;
②根据图象,求关于x的不等式0<-![]() x+10<x的解集;
x+10<x的解集;
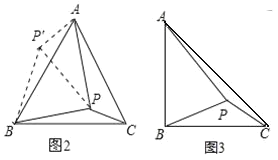
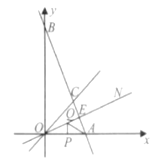
(2)如下图,作∠AOC的平分线ON,若AB⊥ON,垂足为E,ΔOAC的面积为9,且OA=6,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值:若不存在,说明理由.
【答案】(1)①C(4,4) ,②4<x<![]() ;(2) AQ+PQ存在最小值,最小值为3.
;(2) AQ+PQ存在最小值,最小值为3.
【解析】
(1)①根据直线AB和直线OC相交于点C,将两个函数解析式联立,解方程组即为C(4,4);②先求出A点坐标,观察图像即可得出不等式的解集为4<x<![]() ;
;
(2)首先在OC上截取OM=OP,连接MQ,通过SAS定理判定△POQ≌△MOQ,从而得出PQ=MQ,进行等式变换AQ+PQ=AQ+MQ,,即可判断当A、Q、M在同一直线上,且AM⊥0C时,AQ+MQ最小,即AQ+PQ存在最小值;再由ASA定理判定△AEO≌ΔCEO,最后由OC=OA=6,ΔOAC的面积为9,得出AM=3.
(1)①由題意,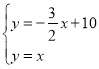
解得:![]()
所以C(4,4)
②把y=0代入![]() ,
,
解得![]()
所以A点坐标为(![]() ,0),
,0),
∵C(4,4),
所以观察图像可得:不等式的解集为4<x<![]() ;
;
(2)由题意,在OC上截取OM=OP,连接MQ,
∵ON平分∠AOC,
∴∠AOQ=∠COQ,
又OQ=OQ.
∴△POQ≌△MOQ(SAS),
∴PQ=MQ,
∴AQ+PQ=AQ+MQ,
当A、Q、M在同一直线上,且AM⊥OC时,AQ+MQ最小,
即AQ+PQ存在最小值
∴AB⊥ON,所以∠AEO=∠CEO,
∴△AEO≌ΔCEO(ASA),
∴OC=OA=6,
∵ΔOAC的面积为9,
∴![]() OC·AM=9,
OC·AM=9,
∴AM=3,
:AQ+PQ存在最小值,最小值为3.