题目内容
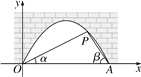
【题目】图中是抛物线型拱桥，P处有一照明灯，水面OA宽4m，从O，A两处观测P处，仰角分别为α，β，tanα＝
，tanβ＝
，以O为原点，OA所在直线为x轴建立直角坐标系．
(1)求点P的坐标；
(2)水面上升1m，水面宽多少(
取1.41，结果精确到0.1m)?
【答案】(1)点P的坐标为
;(2)水面上升1m，水面宽约为2.8m.
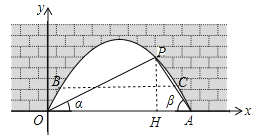
【解析】试题分析：（1）过点P作PH⊥OA于H，如图，设PH=3x，运用三角函数可得OH=6x，AH=2x，根据条件OA=4可求出x，即可得到点P的坐标；
（2）若水面上升1m后到达BC位置，如图，运用待定系数法可求出抛物线的解析式，然后求出y=1时x的值，就可解决问题．
试题解析：（1）过点P作PH⊥OA于H，如图．
设PH=3x，在Rt△OHP中，∵tanα=
，∴OH=6x．
在Rt△AHP中，∵tanβ=
=
，∴AH=2x，∴OA=OH+AH=8x=4，∴x=
，∴OH=3，PH=
，∴点P的坐标为（3， 
）；
（2）若水面上升1m后到达BC位置，如图，过点O（0，0），A（4，0）的抛物线的解析式可设为y=ax（x﹣4），∵P（3， 
）在抛物线y=ax（x﹣4）上，∴3a（3﹣4）=
，解得a=
，∴抛物线的解析式为
．
当y=1时， 
，解得
， 
，∴BC=（
）﹣（
）=
=2×1.41=2.82≈2.8．
答：水面上升1m，水面宽约为2.8米．
练习册系列答案
相关题目
