题目内容
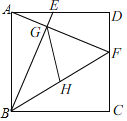
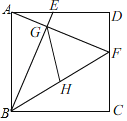
【题目】已知正方形ABCD的边长为4,点E,F分别在AD,DC上,AE=DF=1,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为_____.
【答案】![]() .
.
【解析】
利用正方形的性质证出△ABE≌△DAF,所以∠ABE=∠DAF,进而证得△GBF是直角三角形,利用直角三角形斜边中线等于斜边一半可知GH=![]() BF,最后利用勾股定理即可解决问题.
BF,最后利用勾股定理即可解决问题.
解:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在△ABE和△DAF中,
∵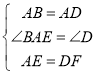 ,
,
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GH=![]() BF,
BF,
∵BC=4、CF=CD﹣DF=4﹣1=3,
∴BF=![]() =5,
=5,
∴GH=![]() BF=
BF=![]() ,
,
故答案为:![]() .
.

 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案【题目】晴晴在某商店购买商品![]() 若干次(每次
若干次(每次![]() 、
、![]() 两种商品都购买),其中第一、二两次购买时,均按标价购买;第三次购买时,商品
两种商品都购买),其中第一、二两次购买时,均按标价购买;第三次购买时,商品![]() 、
、![]() 同时打折,三次购买商品
同时打折,三次购买商品![]() 、
、![]() 的数量和费用如表所示:
的数量和费用如表所示:
购买商品 | 购买商品 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 980 |
第二次购物 | 3 | 7 | 940 |
第三次购物 | 9 | 8 | 912 |
(1)求商品![]() 、
、![]() 的标价;
的标价;
(2)若商品![]() 、
、![]() 的折扣相同,问商店是打几折出售这两种商品的?
的折扣相同,问商店是打几折出售这两种商品的?
(3)在(2)的条件下,若晴晴第四次购物共花去了480元,则晴晴有哪几种购买方案?
【题目】“表格”为初三(1)班全部 43 名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分) | 70 | 80 | 90 |
男生(人) | 5 | 10 | 7 |
女生(人) | 4 | 13 | 4 |
A. 男生的平均成绩小于女生的平均成绩 B. 男生成绩的中位数大于女生成绩的中位数
C. 男生的平均成绩大于女生的平均成绩 D. 男生成绩的中位数小于女生成绩的中位数