题目内容
【题目】(探究发现)
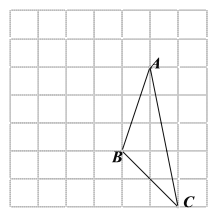
如图1,在△ABC中,点P是内角∠ABC和外角∠ACD的角平分线的交点,试猜想∠P与∠A之间的数量关系,并证明你的猜想.

(迁移拓展)
如图2,在△ABC中,点P是内角∠ABC和外角∠ACD的n等分线的交点,即∠PBC=![]() ∠ABC,∠PCD=
∠ABC,∠PCD=![]() ∠ACD,
∠ACD,
试猜想∠P与∠A之间的数量关系,并证明你的猜想.
(应用创新)
已知,如图3,AD、BE相交于点C,∠ABC、∠CDE、∠ACE的角平分线交于点P,∠A=35°,∠E=25°,则∠BPD= .
【答案】(1)∠A=2∠P;(2)∠A=n∠P;(3)30°.
【解析】
(1)根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和,可求出∠A的度数,根据补角的定义求出∠ACB的度数,根据三角形的内角和即可求出∠P的度数,即可求出结果;
(2)根据已知条件以及一个三角形的外角等于与它不相邻的两个内角和,可求出∠A的度数,根据补角的定义求出∠ACB的度数,根据三角形的内角和即可求出∠P的度数,即可求出结果;
(3)根据(1)的结论即可得到结果.
解:(1)∠A=2∠P,理由如下:
∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
∴∠PBC=![]() ∠ABC,∠PCD=
∠ABC,∠PCD=![]() ∠ACD,
∠ACD,
∵∠ACD是△ABC的外角,∠PCD是△BPC的外角,
∴∠ACD=∠ABC+∠A,∠PCD=∠PBC+∠P,
∴![]() ∠ACD=
∠ACD=![]() ∠ABC+
∠ABC+![]() ∠A,
∠A,
∴![]() ∠ABC+
∠ABC+![]() ∠A=∠PBC+∠P,
∠A=∠PBC+∠P,
∴∠A=2∠P;
(2)∠A=n∠P,理由如下:
∵点P是内角∠ABC和外角∠ACD的n等分线的交点,
∴∠PBC=![]() ∠ABC,∠PCD=
∠ABC,∠PCD=![]() ∠ACE.
∠ACE.
∵∠ACD是△ABC的外角,∠PCD是△BPC的外角,
∴∠ACD=∠ABC+∠A,∠PCD=∠PBC+∠P,
∴![]() ∠ACD=
∠ACD=![]() ∠ABC+
∠ABC+![]() ∠A,
∠A,
∴![]() ∠ABC+
∠ABC+![]() ∠A=∠PBC+∠P,
∠A=∠PBC+∠P,
∴∠A=n∠P;
(3)∵∠ABC、∠CDE、∠ACE的角平分线交于点P,
∴由(1)的结论知,∠BPC=![]() ∠A=
∠A=![]() °,∠CPD=
°,∠CPD=![]() ∠E=
∠E=![]() °,
°,
∴∠BPD=∠BPC+∠DPC=30°,
故答案为:30°.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案