题目内容
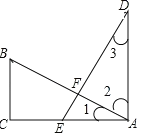
【题目】如图，在Rt△ABC中，∠ACB=90°，E为AC上一点，且AE=BC，过点A作AD⊥CA，垂足为A，且AD=AC，AB、DE交于点F．试判断线段AB与DE的数量关系和位置关系，并说明理由．
【答案】证明见解析.
【解析】试题分析：根据垂直的定义可证得∠DAE=∠ACB=90°，然后根据ASA可证△ABC≌△DEA，从而证得AB=DE，且∠3=∠1，然后根据直角三角形的两锐角互余和等量代换即可证得AB⊥DE.
试题解析：
（1）AB=DE，AB⊥DE.理由如下：
∵AD⊥CA，∴∠DAE=∠ACB=90°．
在△ABC和△DEA中，
，
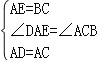∴△ABC≌△DEA（SAS），
∴AB=DE，∠3=∠1．
∵∠DAE=90°，∴∠1+∠2=90°，
∴∠3+∠2=90°，∴∠AFE=90°，
∴AB⊥DE.
练习册系列答案
全能测控一本好卷系列答案
相关题目
