Question

【题目】如图，在□ABCD中，对角线AC、BD交于点O，过点O的直线分别交BC、AD于F、E．若AD=6cm，AB=4cm，OE=2cm，则梯形EFCD的周长是（ ）

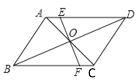
A.16cmB.15cmC.14cmD.12cm

Answer 1

【答案】C

【解析】

根据平行四边形的性质可得CD=AB=4cm，OA=OC，AD∥BC，然后利用AAS证出△EAO≌△FCO，从而得出OE=OF=2cm，AE=CF，然后根据周长公式和等量代换计算即可．

解：∵四边形ABCD为平行四边形，AD=6cm，AB=4cm

∴CD=AB=4cm，OA=OC，AD∥BC

∴∠EAO=∠FCO，∠AEO=∠CFO

在△EAO和△FCO中

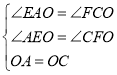
∴△EAO≌△FCO

∴OE=OF=2cm，AE=CF

∴梯形EFCD的周长=EF＋CF＋CD＋DE

=（OE＋OF）＋（AE＋DE）＋CD

=4＋AD＋4

=4＋6＋4

=14cm

故选C．