题目内容
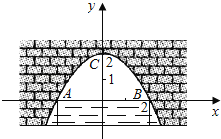
【题目】图中是抛物线形拱桥，当拱顶离水面2m时，水面宽4m，建立如图所示的平面直角坐标系：
（1）求拱桥所在抛物线的解析式；
（2）当水面下降1m时，则水面的宽度为多少？
【答案】（1）y=﹣
x2+2;（2）
【解析】
（1）设出抛物线解析式，由已知条件求出点B、点C的坐标，将B、C的坐标代入抛物线解析式，列方程组求出未知参数即可；（2）令y=﹣1，解出x，即可求出水面的宽度.
解：（1）由题意设抛物线解析式为：y=ax2+b（a≠0），
∵当拱顶离水面2m时，水面宽4m，
∴点C（0，2），点B（2，0），
代入得：
，
解得：
，
∴拱桥所在抛物线的解析式为y=﹣x2+2；
（2）当水位下降1m时，水位纵坐标为﹣1，
令y=﹣1，
则﹣1=﹣x2+2，
解得x=±
，
∴水面宽度为2米.
练习册系列答案
名校课堂系列答案
相关题目
