��Ŀ����
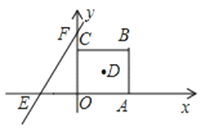
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC�ı߳�Ϊa��ֱ��y=bx+c��x����E����y����F����a��b��c�ֱ�����![]() ��
��![]()
��1����ֱ��y=bx+c�Ľ���ʽ��ֱ��д��������OABC�ĶԽ��ߵĽ���D�����ꣻ
��2��ֱ��y=bx+c��x����������ÿ���ƶ�1����λ���ȵ��ٶ�ƽ�ƣ���ƽ�Ƶ�ʱ��Ϊt�룬���Ƿ����t��ֵ��ʹֱ��EFƽ��������OABC������������ڣ������t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��y=2x��8����D��2,2������2�����ڣ�t=5
��������
��1������ƽ���ķǸ��ԡ����θ�ʽ������������������a��b��c��ֵ���Ӷ����ֱ�߽���ʽ��Ȼ�������B�����꣬�����е����깫ʽ���������D�����ꣻ
��2���������E�����꣬Ȼ���������ɵã���ֱ��ƽ��������OABC�����ʱ��ƽ�ƺ��ֱ�߹���D��Ȼ�����ƽ�ƺ��ֱ�߽���ʽ���Ӷ����ƽ�ƺ�ֱ����x��Ľ������꣬���ɵó����ۣ�
�⣺��1����![]() ��
��![]() ����
����![]()
��![]() ��
��![]()
��ã�a=4��b=2��![]()
��ֱ��EF�Ľ���ʽΪy=2x��8�������εı߳�Ϊ4
���B��������4,4��
�ߵ�DΪ������OABC�ĶԽ��ߵĽ���
���DΪOB���е�
���D��������![]() ��=��2,2��
��=��2,2��
��2�����ڣ�
��y=0����y=2x��8�У���ã�x=-4
���E��������-4,0��
��ƽ�ƺ�Ľ���ʽΪy=2x��m
��ƽ�ƺ��ֱ��ƽ��������OABC�������
��ƽ�ƺ��ֱ�߹���D
����D���������y=2x��m����
2=2��2��m
��ã�m=-2
��ƽ�ƺ�Ľ���ʽΪy=2x��2
��y=0����y=2x��2�����x=1
��ƽ�ƺ���x��Ľ�������Ϊ��1,0����ƽ�ƾ���Ϊ1����-4��=5����λ����
��ƽ��ʱ��t=5��1=5�룮