题目内容
已知:如图△ABC中,∠ACB=90°,点E是边BC上一点,过点E作FE⊥BC(垂足为E)交AB于点F,且EF=AF,以点E为圆心,EC长为半径作⊙E,交BC于点D.
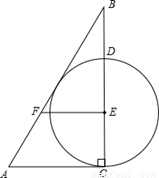
(1)求证:直线AB是⊙E的切线;
(2)设直线AB和⊙E的公共点为G,AC=8,EF=5,连接EG,求⊙E的半径r.
【答案】
(1)证明详见解析;(2)4.
【解析】
试题分析:(1)本题考查切线的判定,要证某一条直线是圆的切线,已知此线过圆上的某点,连接圆心和该点,证垂直即可.如图,过点E作EG⊥AB于点G,连接EA,根据角平分线的性质得到EG=EC即可证得斜边AB是⊙E的切线;
(2)由(1)可知,直线AB与⊙O的公共点G为切点,由切线长定理可得:AG=AC=8.由EF=AF,EF=5,可得:FG=3,在Rt△FEG中由勾股定理易求GE的长度,即⊙E的半径r.
试题解析:
解:(1)过点E作EG⊥AB于点G,连接EA;
∵AF=EF,∠FEA+∠AEC=90°,∠AEC+∠EAC=90°,
∴∠FEA=∠FAE.
∴∠FAE=∠EAC.
∴AE为角平分线.
∴EG=EC.
∴直线AB是⊙E的切线.
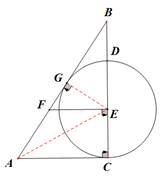
(2)由(1)可知,直线AB与⊙O的公共点G为切点,
∴EG=r,EG⊥AB.
∵∠ACB=90°,EC长为半径,
∴AC是⊙E的切线.
∴AG=AC=8.
∵EF=AF,EF=5,
∴AF=5.
∴FG=AG-AF=8-5=3,
在Rt△EFG中,根据勾股定理,得:
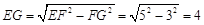 ,
,
∴⊙E的半径r=4.
考点:1、切线的判定;2、切线长定理;3、勾股定理.

练习册系列答案
相关题目
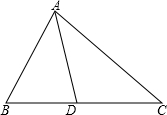 已知,如图△ABC中,AD为△ABC的角平分线,求证:AB•DC=AC•BD.
已知,如图△ABC中,AD为△ABC的角平分线,求证:AB•DC=AC•BD. (1998•河北)已知:如图△ABC中,∠A的平分线AD交BC于D,⊙O过点A,且与BC相切于D,与AB、AC分别相交于E、F,AD与EF相交于G.
(1998•河北)已知:如图△ABC中,∠A的平分线AD交BC于D,⊙O过点A,且与BC相切于D,与AB、AC分别相交于E、F,AD与EF相交于G. 已知:如图△ABC中,∠ACB=90°,D是AC上任意一点,DE⊥AB于E,M,N分别是BD,CE的中点,求证:MN⊥CE.
已知:如图△ABC中,∠ACB=90°,D是AC上任意一点,DE⊥AB于E,M,N分别是BD,CE的中点,求证:MN⊥CE. 已知,如图△ABC中,AB=AC,CD⊥AD于D,CD=
已知,如图△ABC中,AB=AC,CD⊥AD于D,CD= 已知,如图△ABC中,D、E、F分别是三角形三边中点,△ABC的周长为30,面积为48,则△DEF的周长为
已知,如图△ABC中,D、E、F分别是三角形三边中点,△ABC的周长为30,面积为48,则△DEF的周长为