题目内容
（1998•河北）已知：如图△ABC中，∠A的平分线AD交BC于D，⊙O过点A，且与BC相切于D，与AB、AC分别相交于E、F，AD与EF相交于G．（1）求证：AF•FC=GF•DC；
（2）已知AC=6cm，DC=2cm，求FC、GF的长．
分析：（1）根据要证明的线段之间的关系，显然可以构造到三角形AFG和三角形DCF中，根据弦切角定理以及圆周角定理的推论发现∠FDC=∠EFD，则EF∥BC，得到∠AFE=∠C，根据两个角对应相等得到两个三角形相似，从而证明结论．
（2）由切割线定理即可求出CF的长，根据三角形相似即可求出GF的长．
（2）由切割线定理即可求出CF的长，根据三角形相似即可求出GF的长．
解答：（1）证明：连接DF，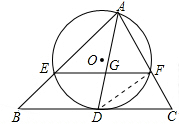
∵AD是△ABC的角平分线，BC是⊙O的切线，∠CDF=∠EFD=∠DAC=∠EAD，
∴EF∥BC．
∴∠C=∠AFE．
∴△AFG∽△DCF，
∴
=
，
即AF•FC=GF•DC；
（2）解：∵BC是⊙O的切线，
∴CD2=CF•AC，
∵AC=6cm，DC=2cm，
∴CF=
，
∴AF=AC-CF=
∵△AFG∽△DCF，
∴
=
，
∴
=
，
∴GF=
．
∵AD是△ABC的角平分线，BC是⊙O的切线，∠CDF=∠EFD=∠DAC=∠EAD，
∴EF∥BC．
∴∠C=∠AFE．
∴△AFG∽△DCF，
∴
| AF |
| DC |
| GF |
| CF |
即AF•FC=GF•DC；
（2）解：∵BC是⊙O的切线，
∴CD2=CF•AC，
∵AC=6cm，DC=2cm，
∴CF=
| 2 |
| 3 |
∴AF=AC-CF=
| 16 |
| 3 |
∵△AFG∽△DCF，
∴
| AF |
| DC |
| GF |
| CF |
∴
| ||
| 2 |
| GF | ||
|
∴GF=
| 16 |
| 9 |
点评：本题考查弦切角定理、圆周角定理以及切割线定理的运用，此类题一般首先能够把线段放到两个三角形中，熟练运用相似三角形的判定和性质．
练习册系列答案
相关题目
（1998•河北）已知：如图弦AB经过⊙O的半径OC的中点P，且AP=2，PB=3，则是⊙O的半径等于（ ）
（1998•河北）已知：如图，在⊙O中，直径AB⊥CD，BE切⊙O于B，且BE=BC，CE交AB于F、交⊙O于M，连接MO并延长，交⊙O于N．则下列结论中，正确的是（ ）