Question

【题目】在矩形中，，，点是上一点，翻折，得，点落在上，则的值是（ ）

A. 1B.

C. D.

Answer 1

【答案】D

【解析】

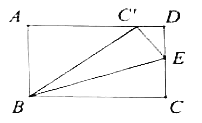
设CE=x，由矩形的性质得出AD=BC=5，CD=AB=3，∠A=∠D=90°．由折叠的性质得出BC`=BC=5，EC`=CE=x，DE=CD-CE=3-x．在Rt△ABC`中利用勾股定理求出AC`的长度，进而求出DC`的长度；然后在Rt△DEC`中根据勾股定理列出关于x的方程，即可解决问题．

设CE=x.

∵四边形ABCD是矩形，

∴AD=BC=5,CD=AB=3,∠A=∠D=90°.

∵将△BCE沿BE折叠，使点C恰好落在AD边上的点C`处，

∴B C`=BC=5，E C`=CE=x，DE=CDCE=3x.

在Rt△AB C`中，由勾股定理得：

A C`=53=16，

∴A C`=4，D C`=54=1.

在Rt△DE C`中，由勾股定理得：

E C`=DE+D C`，

即x=(3x) +1，

解得：x=.

故选D