题目内容
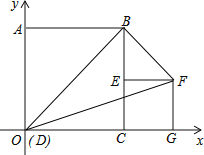
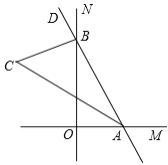
【题目】如图,两直线 OM 与 ON 垂直,点 A,B 分别在射线 OM,ON 上移动,BC 平分∠DBO,BC 与∠OAB 的平分线 AC 交于点 C.
(1)若∠BAO=60°,求∠C 的度数;
(2)若∠BAO 的度数为 x 度,求∠C 的度数.
【答案】(1)45;(2)45°
【解析】
根据AC是角平分线结合三角形内角和定理可以用∠BAO表示出∠BAC与∠OBA,从而可以求出答案,解出(1);(2)中将∠BAO的度数换为X度即可,思路同(1)推理解答即可
解:(1)∵∠BAO=60,∴∠DBO=150,
∵BC 平分∠DBO,∴∠CBA=105,
∵AC 平分∠OAB,
∴∠C=180-105-30=45.
(2)因为∠BAO=x 度,则∠BAC=![]() 度,∠OBA=90°-x°
度,∠OBA=90°-x°
所以∠DBO=180°-∠OBA=180°-(90°-x°)=90°+x°
因为BC平分∠DBO,所以∠CBA=![]() =
=![]()
所以∠C=180°-∠CBA-∠BAC=![]()

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目