题目内容
【题目】（问题探究）
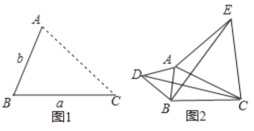
（1）如图①已知锐角△ABC，分别以AB、AC为腰，在△ABC的外部作等腰Rt△ABD和Rt△ACE,连接CD、BE，是猜想CD、BE的大小关系_____________ ；（不必证明）
（深入探究）
（2）如图②△ABC、△ADE都是等腰直角三角形，点D在边BC上（不与B、C重合），连接EC，则线段 BC，DC，EC 之间满足的等量关系式为________________ ；（不必证明） 线段 AD2，BD2，CD2之间满足的等量关系，并证明你的结论；
（拓展应用）
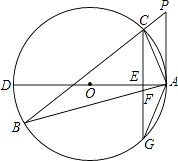
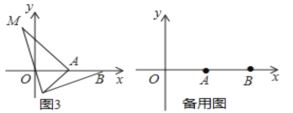
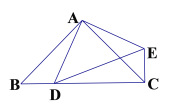
（3）如图③，在四边形 ABCD 中，∠ABC=∠ACB=∠ADC=45°．若 BD=9，CD=3，
求 AD 的长．
① ② ③
【答案】（1）CD=BE；（2）BC=CD+EC，BD2+CD2=2AD2，理由见解析；（3）AD =6.
【解析】
（1）如图所示，结论：CD = BE．只要证明△DAC≌△BAE即可；
（2）结论：BC=CD+EC， BD2+CD2=2AD2，依据△DAB≌△EAC可得BD=CE,AD=AE, ∠B=∠ACE=45°,因此CE +CD =AD +AE ,即可得出结论；
（3）作AE⊥AD，使AE=AD，连接CE，DE，证明△BAD≌△CAE，得到BD=CE=9，根据勾股定理计算算出DF=
,从而得到AD=AF=6.
解：（1）CD=BE；
（2）BC=CD+EC，
BD2+CD2=2AD2，理由如下：
∵∠BAC=∠DAE=90°，
∴∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE，
在△BAD和△CAE中，
，
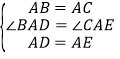∴△BAD≌△CAE，
∴BD=CE，∠ACE=∠B，
∴∠DCE=90°，
∴CE2+CD2=ED2，
在Rt△ADE中，AD2+AE2=ED2，又AD=AE，
∴BD2+CD2=2AD2；
（3）作AE⊥AD，使AE=AD，连接CE，DE，
∵∠BAC+∠CAD=∠DAE+∠CAD，
即∠BAD=∠CAE，
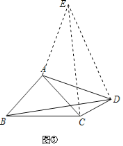
在△BAD与△CAE中，
，
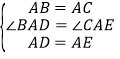∴△BAD≌△CAE（SAS），
∴BD=CE=9，
∵∠ADC=45°，∠EDA=45°，
∴∠EDC=90°，
∴DE=
=6
，
∵∠DAE=90°，
∴AD=AE=
DE=6．
