题目内容
【题目】如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G. 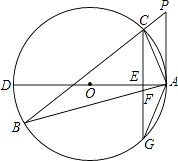
(1)判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AFAB;
(3)若⊙O的直径为10,AC=2 ![]() ,AB=4
,AB=4 ![]() ,求△AFG的面积.
,求△AFG的面积.
【答案】
(1)解:PA与⊙O相切.理由:
连接CD,

∵AD为⊙O的直径,
∴∠ACD=90°,
∴∠D+∠CAD=90°,
∵∠B=∠D,∠PAC=∠B,
∴∠PAC=∠D,
∴∠PAC+∠CAD=90°,
即DA⊥PA,
∵点A在圆上,
∴PA与⊙O相切
(2)解:证明:如图2,连接BG,
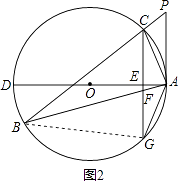
∵AD为⊙O的直径,CG⊥AD,
∴ ![]() =
= ![]() ,
,
∴∠AGF=∠ABG,
∵∠GAF=∠BAG,
∴△AGF∽△ABG,
∴AG:AB=AF:AG,
∴AG2=AFAB
(3)解:解:如图3,连接BD,
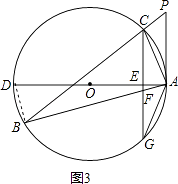
∵AD是直径,
∴∠ABD=90°,
∵AG2=AFAB,AG=AC=2 ![]() ,AB=4
,AB=4 ![]() ,
,
∴AF= ![]() =
= ![]() ,
,
∵CG⊥AD,
∴∠AEF=∠ABD=90°,
∵∠EAF=∠BAD,
∴△AEF∽△ABD,
∴ ![]() ,
,
即 ![]() ,
,
解得:AE=2,
∴EF= ![]() =1,
=1,
∵EG= ![]() =4,
=4,
∴FG=EG﹣EF=4﹣1=3,
∴S△AFG= ![]() FGAE=
FGAE= ![]() ×3×2=3.
×3×2=3.
【解析】(1)首先连接CD,由AD为⊙O的直径,可得∠ACD=90°,然后由圆周角定理,证得∠B=∠D,由已知∠PAC=∠B,可证得DA⊥PA,继而可证得PA与⊙O相切.(2)首先连接BG,易证得△AFG∽△AGB,然后由相似三角形的对应边成比例,证得结论;(3)首先连接BD,由AG2=AFAB,可求得AF的长,易证得△AEF∽△ABD,即可求得AE的长,继而可求得EF与EG的长,则可求得答案.

【题目】某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成). 安全知识测试成绩频数分布表
组别 | 成绩x(分数) | 组中值 | 频数(人数) |
1 | 90≤x<100 | 95 | 10 |
2 | 80≤x<90 | 85 | 25 |
3 | 70≤x<80 | 75 | 12 |
4 | 60≤x<70 | 65 | 3 |

(1)完成频数分布直方图;
(2)这个样本数据的中位数在第组;
(3)若将各组的组中值视为该组的平均成绩,则此次测试的平均成绩为;
(4)若将90分以上(含90分)定为“优秀”等级,则该县10000名初中生中,获“优秀”等级的学生约为人.